同志社大学(理系) 2022年 問題4
$定数 \ a\ は \ \ 0 < a < 1 \ \ とする。\theta \ を実数とし、関数 \ f(\theta)=\cfrac{1-a^2}{2\pi(1+a^2-2a\cos \theta)} \ \ とする。$
$次の問いに答えよ。$
$\qquad (1)\ \ t=\tan \cfrac{\theta}{2}\ \ (-\pi < \theta < \pi) \ \ とおいて、f(\theta) \ を \ t\ の式で表す。この \ t\ の式を \ f_1(t)\ とすると$
$\qquad \quad t\ の関数 \ f_1(t)\ はある定数 \ b\ を用いて、f_1(t)=\cfrac{b(1+t^2)}{2\pi(b^2+t^2)} \ \ と表せる。b\ を \ a\ の式で表せ。$
$\qquad (2)\ \ g(\theta)\ は連続で \ 2\pi \ を周期とする周期関数とする。c\ を実数とするとき、$
\[\quad 等式 \int _0^{2\pi}g(\theta)d\theta =\int _c^{c+2\pi}g(\theta)d\theta \ \ が成り立つことを示せ。\]
$\qquad (3)\ \ -\pi < \theta <\pi \ \ のとき、実数 \ u\ \ (-\cfrac{\pi}{2} u < \cfrac{\pi}{2})\ \ は(1)の \ b\ を用いて \quad b\tan u=\tan \cfrac{\theta}{2} \ \ を満たすとする。$
$\qquad \quad このとき、f(\theta)\ を \ u\ で表した式を \ f_2(u)\ とし、式 \ f_2(u) \cfrac{d\theta}{du} \ \ の値を \ h\ とする。h\ を求めよ。$
\[(4)\ \ r\ を実数とする。定積分\ \ \int _0^{2\pi} f(\theta -r)\cos \theta d\theta \ \ を \ a\ と \ r\ の式で表せ。ただし、必要ならば(3)の\]
\[\quad h\ に対して、等式 \ \ \int _{-\pi}^{\pi} f(\theta)d\theta =\pi h \ \ が成り立つことを証明なしで用いてよい。\]
$(解説)$
$(1)\ \ この変換は三角関数の定積分での必須事項です。$
$(2)\ \ 周期関数の1周期分の定積分はどの区間をとっても一定ですが、その証明は工夫が必要です。$
$\qquad この公式は(4)で使われます。$
$(3)\ \ f_1(t)\ の分母から \ \ t=b\tan u \ \ と変換します。$
$(4)\ \ \theta -r=\omega \ \ とおいて、\cos(r+\omega )\ \ を展開します。f(\theta)\ が連続であることを示す必要があります。$
$\qquad なお、この等式は研究として示します。$
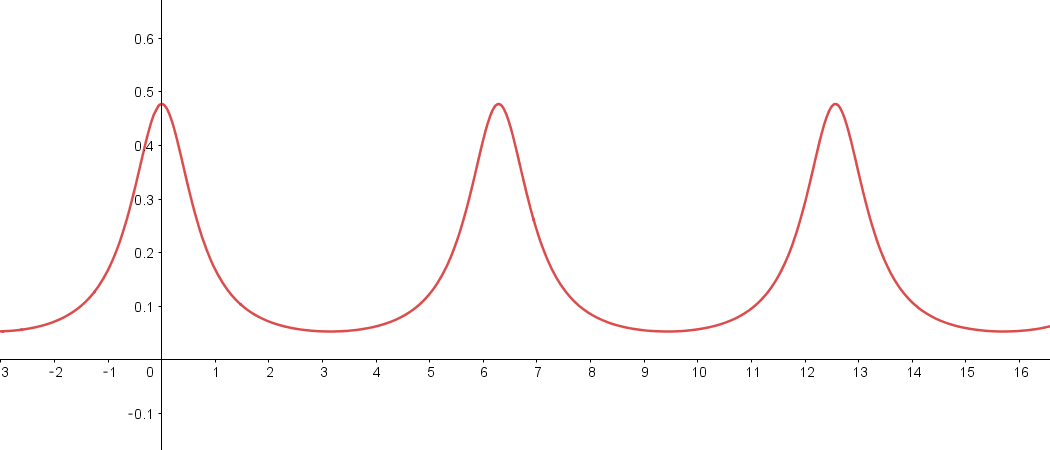
$右図は、a=\cfrac{1}{2} \ \ のときの \ \ y=f(\theta)\ \ のグラフです。$
$これでイメージがつかめると思います。$
$まず、次の \ 2\ 点を確認しておきましょう。$
(i)$\ \ f(\theta)\ は \ 2\pi \ を周期とする周期関数です。$
(ii)$\ \ (1+a^2)-2a=(1-a)^2 > 0 \quad だから \quad 1+a^2 > 2a \geqq 2a\cos \theta $
$\ \ \therefore \ \ 1+a^2-2a\cos \theta >0 \quad よって \quad f(\theta) \ \ は連続関数です。$
(1)
$\qquad \cos \theta =\cos ^2 \cfrac{\theta}{2}- \sin ^2 \cfrac{\theta}{2}=\cfrac{\cos ^2 \cfrac{\theta}{2}- \sin ^2 \cfrac{\theta}{2}}{\cos ^2 \cfrac{\theta}{2}+ \sin ^2 \cfrac{\theta}{2}}=\cfrac{1-\tan ^2 \cfrac{\theta}{2}}{1+\tan ^2 \cfrac{\theta}{2}}=\cfrac{1-t^2}{1+t^2}$
\begin{eqnarray*} f_1(t) &=&\cfrac{1-a^2}{2\pi\big(1+a^2-2a \times \dfrac{1-t^2}{1+t^2}\big)}\\ \\ &=&\cfrac{(1-a^2)(1+t^2)}{2\pi\big((1+a^2)(1+t^2)-2a(1-t^2)\big)}\\ \\ &=&\cfrac{(1-a^2)(1+t^2)}{2\pi\big((1+a^2-2a+(1+a^2+2a)t^2)\big)}\\ \\ &=&\cfrac{(1-a^2)(1+t^2)}{2\pi\big((1-a)^2+(1+a)^2t^2\big)}\\ \\ &=&\cfrac{\dfrac{1-a^2}{(1+a)^2}(1+t^2)}{2\pi\big((\dfrac{1-a}{1+a})^2+t^2\big)}\\ \\ &=&\cfrac{\dfrac{1-a}{1+a}(1+t^2)}{2\pi\big((\dfrac{1-a}{1+a})^2+t^2\big)}\\ \end{eqnarray*}
$\qquad よって \quad b=\cfrac{1-a}{1+a} \quad ととると \quad f_1(t)=\cfrac{b(1+t^2)}{2\pi(b^2+t^2)} \quad と表せる。$
(2)

\[\int _c^{c+2\pi}g(\theta)d\theta =\int _c^{2\pi}g(\theta)d\theta +\int _{2\pi}^{c+2\pi}g(\theta)d\theta \]
$第2項で \quad \theta -2\pi=t \quad とおくと \ \ g(\theta) \ \ は$
$2\pi\ \ を周期とする周期関数だから$
\[第2項=\int _0^c g(2\pi +t)dt =\int _0^c g(2\pi + \theta)d\theta=\int _0^c g(\theta)d\theta \]
\[よって \quad 右辺=\int _c^{2\pi}g(\theta)d\theta +\int _0^c g(\theta)d\theta=\int _0^{2\pi}g(\theta)d\theta \quad となり\]
\[\int _0^{2\pi}g(\theta)d\theta =\int _c^{c+2\pi}g(\theta)d\theta \quad が成り立つ\]
$とくに$
\[c=-\pi \quad とおくと \quad \int _0^{2\pi}g(\theta)d\theta =\int _{-\pi}^{\pi} g(\theta)d\theta \]
\[c=-r \quad とおくと \quad \int _0^{2\pi}g(\theta)d\theta =\int _{-r}^{2\pi-r} g(\theta)d\theta \]
\[したがって \quad \int _{-r}^{2\pi-r} g(\theta)d\theta =\int _{-\pi}^{\pi} g(\theta)d\theta \quad がいえるがこの等式は(4)で使われます。\]
(3)
$\qquad b\tan u=\tan \cfrac{\theta}{2} \quad を \ u\ で微分すると \quad \cfrac{b}{\cos ^2 u}=\cfrac{1}{2\cos ^2\dfrac{\theta}{2}}\cfrac{d\theta}{du}$
$\qquad \cfrac{d\theta}{du}=\cfrac{2b\cos ^2\dfrac{\theta}{2}}{\cos ^2 u}=\cfrac{2b}{\cos ^2 u(1+\tan ^2\dfrac{\theta}{2})}=\cfrac{2b}{\cos ^2 u(1+b^2\tan ^2 u)}$
$また$
\begin{eqnarray*} f_2(u) &=&f_1(t)\\ \\ &=&\cfrac{b(1+t^2)}{2\pi(b^2+t^2)} \hspace{3em} t=b\tan u \quad とおいて\\ \\ &=&\cfrac{b(1+b^2\tan ^2u )}{2\pi(b^2+b^2 \tan ^2u )}\\ \\ &=&\cfrac{1+b^2\tan ^2u }{2\pi b(1+ \tan ^2u )}\\ \\ &=&\cfrac{1}{2\pi b}\cos ^2 u(1+b^2\tan ^2u) \\ \end{eqnarray*} $よって$
$\qquad h=f_2(u)\cfrac{d\theta}{du}=\cfrac{1}{2\pi b} \cos ^2 u(1+b^2\tan ^2u ) \times \cfrac{2b}{\cos ^2 u(1+b^2\tan ^2 u)}=\cfrac{1}{\pi}$
(4)
\[I=\int _0^{2\pi} f(\theta -r)\cos \theta d\theta \quad で \quad \theta -r=\omega \quad とおくと \quad d\theta=d\omega \quad だから\] \begin{eqnarray*} I &=&\int _{-r}^{2\pi -r} f(\omega)\cos (\omega + r) d\omega\\ \\ &=&\int _{-r}^{2\pi -r} f(\omega)(\cos \omega \cos r - \sin \omega \sin r) d\omega\\ \\ &=&\cos r \int _{-r}^{2\pi -r} f(\omega)\cos \omega d\omega -\sin r \int _{-r}^{2\pi -r} f(\omega)\sin \omega d\omega \\ \end{eqnarray*} $\hspace{4em} f(\omega)\cos \omega ,\quad f(\omega)\sin \omega \quad はともに連続で、\ 2\pi \ を周期とする周期関数だから(2)で示したことから$
$1項目は$
\begin{eqnarray*} & &\int _{-r}^{2\pi -r} f(\omega)\cos \omega d\omega\\ \\ &=&\int _{-\pi}^{\pi} f(\omega)\cos \omega d\omega \\ \\ &=&\int _{-\pi}^{\pi} \cfrac{(1-a^2)\cos \omega }{2\pi(1+a^2-2a\cos \omega)}d\omega \\ \\ &=&\cfrac{1-a^2}{2\pi(-2a)} \int _{-\pi}^{\pi} \cfrac{-2a\cos \omega }{1+a^2-2a\cos \omega}d\omega \\ \\ &=&-\cfrac{1-a^2}{4\pi a} \int _{-\pi}^{\pi} \cfrac{1+a^2-2a\cos \omega -(1+a^2)}{1+a^2-2a\cos \omega}d\omega \\ \\ &=&-\cfrac{1-a^2}{4\pi a} \int _{-\pi}^{\pi} \big(1-\cfrac{1+a^2}{1+a^2-2a\cos \omega}\big)d\omega \\ \\ &=&-\cfrac{1-a^2}{4\pi a} \times 2\pi + \cfrac{1-a^2}{4\pi a} \int _{-\pi}^{\pi} \cfrac{1+a^2}{1+a^2-2a\cos \omega}d\omega \\ \\ &=&-\cfrac{1-a^2}{2a} + \cfrac{1+a^2}{2a} \int _{-\pi}^{\pi} \cfrac{1-a^2}{2\pi(1+a^2-2a\cos \omega)}d\omega \\ \\ &=&-\cfrac{1-a^2}{2a} + \cfrac{1+a^2}{2a} \int _{-\pi}^{\pi} f(\omega)d\omega \\ \\ &=&-\cfrac{1-a^2}{2a} + \cfrac{1+a^2}{2a} \pi h\\ \\ &=&-\cfrac{1-a^2}{2a} + \cfrac{1+a^2}{2a} \times 1\\ \\ &=&a \end{eqnarray*}
$第2項目は$
$\qquad f(\omega)\sin \omega d\omega \ \ は \ f(\omega)\ が偶関数、\sin \omega \ \ が奇関数だから \ \ f(\omega)\sin \omega \ \ は奇関数となって$
\[\int _{-r}^{2\pi -r} f(\omega)\sin \omega d\omega =\int _{-\pi}^{\pi} f(\omega)\sin \omega d\omega =0\]
$したがって \quad I=a\cos r$
$(研究)$
\[証明なしで用いてよいという等式 \quad \int _{-\pi}^{\pi} f(\theta)d\theta =1 \quad を導きましょう。\] $\quad 変数変換は(1),(3)で示されています。$
\begin{eqnarray*} I &=&\int _{-\pi}^{\pi} f(\theta)d\theta\\ \\ &=&\cfrac{1-a^2}{2\pi} \int _{-\pi}^{\pi}\cfrac{d\theta}{1+a^2-2a\cos \theta}\\ \end{eqnarray*} \[\hspace{3em} t=\tan \cfrac{\theta}{2} \quad とおくと \quad d\theta=\cfrac{2}{1+t^2}dt \qquad \begin{array}{c|c} \theta & \ -\pi \ \ \rightarrow \pi \quad \\ \hline t & -\infty \rightarrow \infty \\ \end{array} \] \begin{eqnarray*} I &=&\cfrac{1-a^2}{2\pi} \int _{-\infty}^{\infty}\cfrac{1}{1+a^2-2a \times \dfrac{1-t^2}{1+t^2}} \times \cfrac{2}{1+t^2}dt\\ \\ &=&\cfrac{1-a^2}{\pi} \int _{-\infty}^{\infty}\cfrac{dt}{(a+1)^2t^2+(a-1)^2}\\ \end{eqnarray*} $\hspace{5em} b=\cfrac{a-1}{a+1} \quad とおくと \ \ (b < 0 \ に注意)$
\begin{eqnarray*} I &=&\cfrac{2(1-a)}{\pi(1+a)} \int _0^{\infty}\cfrac{dt}{t^2+b^2}\\ \end{eqnarray*} \[\hspace{3em} t=b\tan u \quad とおくと \quad dt=\cfrac{bdu}{\cos ^2 u} \qquad \begin{array}{c|c} t & \ 0\ \ \rightarrow \infty \quad \\ \hline u & \ 0 \rightarrow -\cfrac{\pi}{2} \\ \end{array} \] \begin{eqnarray*} I &=&\cfrac{2(1-a)}{\pi(1+a)} \int _0^{-\scriptsize{\cfrac{\pi}{2}}}\cfrac{1}{b^2\tan ^2 u +b^2} \times \cfrac{bdu}{\cos ^2 u}\\ \\ &=&\cfrac{2(1-a)}{\pi(1+a)} \times \cfrac{1}{b} \int _0^{-\scriptsize{\cfrac{\pi}{2}}} \cos ^2 u \cdot \cfrac{du}{\cos ^2 u}\\ \\ &=&\cfrac{2(1-a)}{\pi(1+a)} \times \cfrac{a+1}{a-1} \int _0^{-\scriptsize{\cfrac{\pi}{2}}} du\\ \\ &=&-\cfrac{2}{\pi} \times (-\cfrac{\pi}{2})\\ \\ &=&1 \end{eqnarray*}
メインメニュー に戻る