千葉大学(理系) 2021年 問題6
$多項式 \ f_n(x),\ \ g_n(x)\ \ (n=1,2,3,\cdots)\ を条件$
$\qquad f_1(x)=x,\quad g_1(x)=1,$
$\qquad f_{n+1}(x)=f_n(x)+xg_n(x),\quad g_{n+1}(x)=g_n(x)-xf_n(x)$
$で定める。$
$(1)\ \ 正の整数 \ n\ に対して、等式 \quad \{f_{n+1}(x)\}'=(n+1)g_n(x),\quad \{g_{n+1}(x)\}'=-(n+1)f_n(x)$
$\quad が成り立つことを示し、多項式 \ f_n(x)\ の次数を求めよ。$
$(2)\ \ 正の整数 \ n\ に対して、区間 \ \ -\cfrac{\pi}{2} < \theta < \cfrac{\pi}{2} \ \ において等式$
$\qquad \sin n\theta =f_n(\tan \theta)\cos ^n\theta ,\quad \cos n\theta =g_n(\tan \theta)\cos ^n\theta \quad が成り立つことを示せ。$
$(3)\ \ 正の整数 \ nと実数 \ a\ に対して、方程式 \ \ f_n(x)=ag_n(x)\ \ の異なる実数解の個数を求めよ。$
$(解説)$
$(1)\ \ 数学的帰納法で証明します。次数については、初めの何項かを計算すると推測できます。$
$(2)\ \ 右辺は \ \ x=\tan \theta \ \ と置いた式ですが、やはり初めの何項かを計算すると等式の意味が理解できると思います。$
$\quad 数学的帰納法で証明します。$
$(3)\ \ a=\tan n\theta \ \ と変形し、交点の個数を調べます。$
$なお、(2)を定義式として、問題文の漸化式と(1)を導くこともできますので、後ろに付けました。$
(1)
$見易くするために、f_n(x),\ \ g_n(x),\ \ \{f_n(x)\}',\ \ \{g_n(x)\}'\ を簡単に \ \ f_n,\ g_n, \ f_n',\ g_n'\ と書くことにします。$
$まず、はじめの数項を与えられた漸化式から求めてみます。$
$\qquad f_1=x,\quad g_1=1 \quad より$
$\qquad f_2=f_1+xg_1=x+x=2x,\qquad g_2=g_1-xf_1=1-x^2$
$\qquad f_3=f_2+xg_2=2x+x(1-x^2)=3x-x^3,\qquad g_3=g_2-xf_2=(1-x^2)-x \times 2x=1-3x^2$
$\hspace{3em} \vdots $
$(A):f_{n+1}'(x)=(n+1)g_n(x),\qquad (B):g_{n+1}'(x)=-(n+1)f_n(x) \quad が成りたつことを数学的帰納法で示します。$
(i)$\ \ n=1\ \ のとき$
$\qquad (A)について \quad 左辺=f_2'=(2x)'=2,\qquad 右辺=2g_1=2 \quad よって成りたつ。$
$\qquad (B)について \quad 左辺=g_2'=(1-x^2)'=-2x,\qquad 右辺=-2f_1=-2x \quad よって成りたつ。$
(ii)$\ \ n=k \ \ のとき成りたつとすると$
$\qquad (A):f_{k+1}'(x)=(k+1)g_k,\qquad (B):g_{k+1}'(x)=-(k+1)f_k$
$このとき$
$\quad (A)について$
\begin{eqnarray*} f_{k+2}' &=&(f_{k+1}+xg_{k+1})'\\ &=&f_{k+1}'+g_{k+1}+xg_{k+1}'\\ &=&(k+1)g_k+g_{k+1}-(k+1)xf_k\\ &=&(k+1)g_k + g_{k+1} -(k+1)(g_k-g_{k+1})\\ &=&(k+2)g_{k+1}\\ \end{eqnarray*} $\quad よって \ \ n=k+1\ \ のときも成りたつ。$
$\quad (B)について$
\begin{eqnarray*} g_{k+2}' &=&(g_{k+1}-xf_{k+1})'\\ &=&g_{k+1}'-f_{k+1}-xf_{k+1}'\\ &=&-(k+1)f_{k}-f_{k+1} -(k+1)xg_k\\ &=&-(k+1)f_k-f_{k+1}-(k+1)(f_{k+1} -f_k)\\ &=&-(k+2)f_{k+1}\\ \end{eqnarray*} $\quad よって \ \ n=k+1 \ \ のときも成りたつ。$
$f_n(x)\ と \ g_n(x)\ の次数をそれぞれ \ \ p_n,\ \ q_n \ \ とおくと$
$\qquad p_1=1,\quad q_1=0,\quad p_2=1,\quad q_2=2,\quad \cdots $
$上で証明した \quad (A):f_{n+1}'(x)=(n+1)g_n(x),\qquad (B):g_{n+1}'(x)=-(n+1)f_n(x) \quad より$
$多項式は微分すると次数が \ 1\ 下がることから \quad p_{n+1}=q_n+1,\qquad q_{n+1}=p_n+1$
$この漸化式から \quad (p_n,q_n)\ \ は順に \ (1,\ 0),\ (1,\ 2),\ (3,\ 2),\ (3,\ 4),\ (5,\ 4),\ (5,\ 6),\ (7,\ 6),\ (7,\ 8),\ \cdots $
$これらから、容易に \ \ p_n,\ \ q_n \ \ が推測できるが、漸化式から考えてみましょう。$
$\qquad p_{n+2}=q_{n+1}+1=(p_n+1)+1=p_n + 2$
(i)$\ \ nが奇数のとき$
$\quad p_n=n \ \ と推測できるがこれが正しいことを数学的帰納法で証明すると$
$\qquad n=1\ \ のとき \quad p_1=1 \quad だから成りたつ。$
$\qquad n=k\ \ のとき成りたつとすると \quad p_k=k$
$\qquad このとき \quad p_{k+2}=p_k+2=k+2 \quad だから \quad n=k+2 \quad のときも成りたつ。$
(ii)$\ \ nが偶数のとき$
$\quad p_n=n-1 \ \ と推測できるが、数学的帰納法による証明は省略します。$
$なお、全く同様にして \qquad q_{n+2}=q_n+2 $
$\quad n\ が奇数のとき \quad q_n=n-1, \qquad n\ が偶数のとき \quad q_n=n$
(2)
$\quad (A):\sin n\theta =f_n(\tan \theta)\cos ^n\theta ,\qquad (B):\cos n\theta =g_n(\tan \theta)\cos ^n\theta \quad が成りたつことを数学的帰納法で証明します。$
(i)$\ \ n=1 \ \ のとき$
$\quad (A)について$
$\qquad 左辺=\sin \theta ,\qquad 右辺=f_1(\tan \theta)\cos \theta=\tan \theta \cos \theta =\sin \theta \quad よって成りたつ。$
$\quad (B)について$
$\qquad 左辺=\cos \theta ,\qquad 右辺=g_1(\tan \theta)\cos \theta= \cos \theta \quad よって成りたつ。$
(ii)$\ \ n=k \ \ のとき成りたつとすると$
$\quad (A):\sin k\theta =f_k(\tan \theta)\cos ^k\theta ,\qquad (B):\cos k\theta =g_k(\tan \theta)\cos ^k\theta $
$このとき$
$\quad (A)について$
\begin{eqnarray*} & &\sin (k+1)\theta \\ &=&\sin (k\theta + \theta)\\ &=&\sin k\theta \cos \theta +\cos k\theta \sin \theta \\ &=&f_k(\tan \theta)\cos ^k\theta \cos \theta + g_k(\tan \theta)\cos ^k\theta \sin \theta \\ &=&\{f_k(\tan \theta) + \tan \theta g_k(\tan \theta)\}\cos ^{k+1}\theta \\ &=&f_{k+1}(\tan \theta)\cos ^{k+1}\theta \\ \end{eqnarray*} $よって \quad n=k+1\ \ のときも成りたつ。$
$\quad (B)について$
\begin{eqnarray*} & &\cos (k+1)\theta \\ &=&\cos (k\theta + \theta)\\ &=&\cos k\theta \cos \theta -\sin k\theta \sin \theta \\ &=&g_k(\tan \theta)\cos ^k\theta \cos \theta - f_k(\tan \theta)\cos ^k\theta \sin \theta \\ &=&\{g_k(\tan \theta) - \tan \theta f_k(\tan \theta)\}\cos ^{k+1}\theta \\ &=&g_{k+1}(\tan \theta)\cos ^{k+1}\theta \\ \end{eqnarray*} $よって \quad n=k+1\ \ のときも成りたつ。$
(3)
$\quad \sin n\theta =f_n(\tan \theta)\cos ^n\theta ,\qquad \cos n\theta =g_n(\tan \theta)\cos ^n\theta \quad で \quad \tan \theta =x \quad とおくと$
$\qquad f_n(x)=\cfrac{\sin n\theta}{\cos ^n\theta},\qquad g_n(x)=\cfrac{\cos n\theta}{\cos ^n \theta} $
$\quad f_n(x)=ag_n(x) \quad より \quad \sin n\theta =a \cos n\theta \quad \therefore \ \ a=\tan n\theta$
$\qquad \tan \theta =x \ \ は区間 \ \ -\cfrac{\pi}{2} < \theta < \cfrac{\pi}{2}\ \ では \ \ \theta \ \ と \ x\ は \ 1\ 対 \ 1\ に対応するから$
$\qquad f_n(x)=ag_n(x) \quad の異なる実数解 \ x\ の個数は、\quad a=\tan n\theta \quad をみたす \ \ \theta \ \ の個数に等しい。$
$\quad したがって、y=a\ \ と,\ \ y=\tan n\theta \quad の交点の個数を調べればよい。$
$なお、y=\tan n\theta \ \ は奇関数だからグラフは原点に関して対称であるので、a > 0 \ \ と \ \ a < 0\ \ の交点の個数は一致する。$
$また、y=\tan n\theta \ \ のグラフは、y=\tan \theta \ \ のグラフを \ \ \theta 軸方向に \ \ \cfrac{1}{n}\ 倍に縮小したものである。$
(i)$\ \ nが奇数のとき$
$\hspace{6em}n=1\ \ のとき \hspace{10em}n=3\ \ のとき \hspace{10em}n=5\ \ のとき$
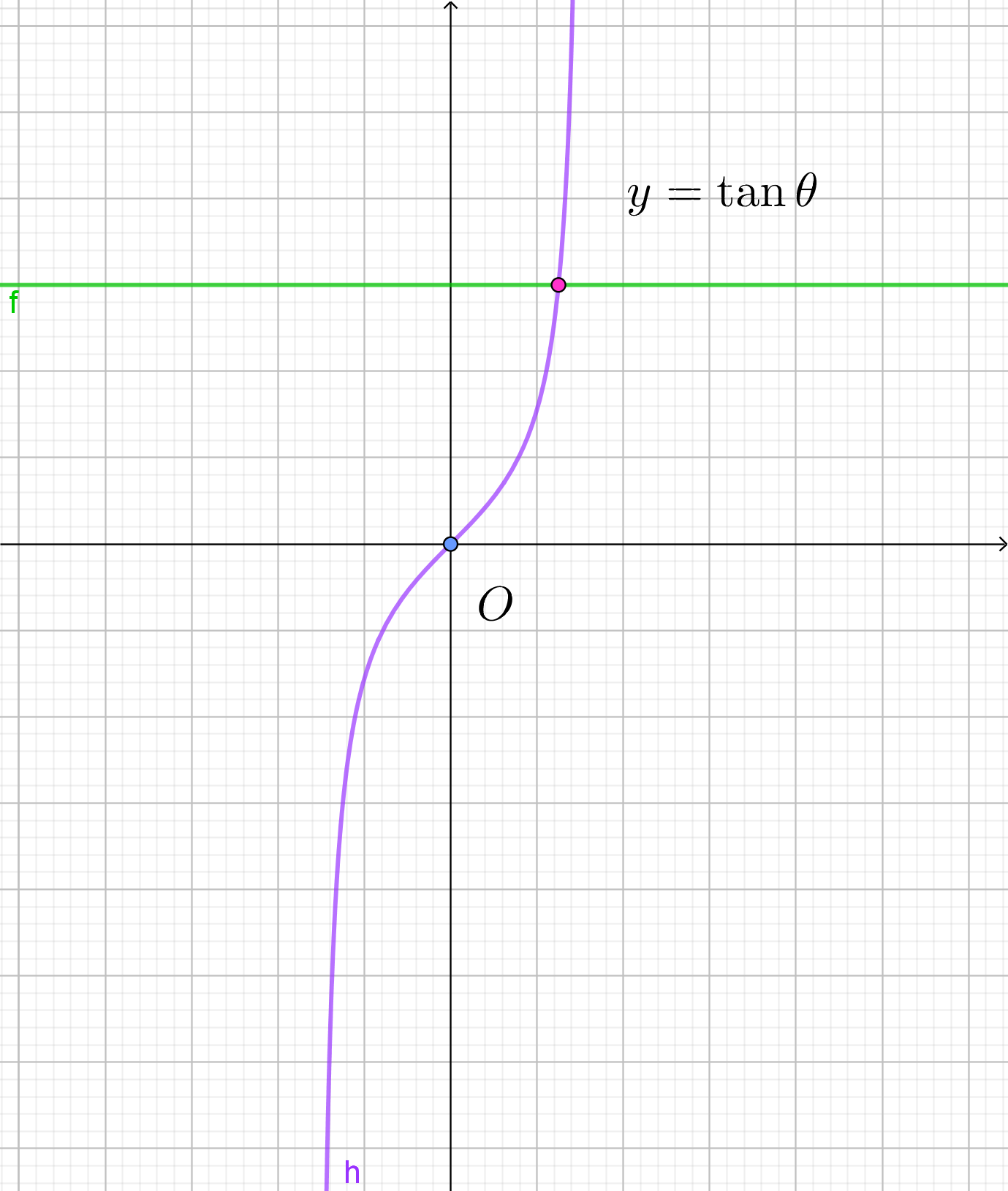


$\quad 交点の個数は、a\ の値にかかわらず、n\ 個であるから、実数解の個数も \ n\ 個である。$
(ii)$\ \ nが偶数のとき$
$\hspace{6em}n=2\ \ のとき \hspace{10em}n=4\ \ のとき \hspace{10em}n=6\ \ のとき $

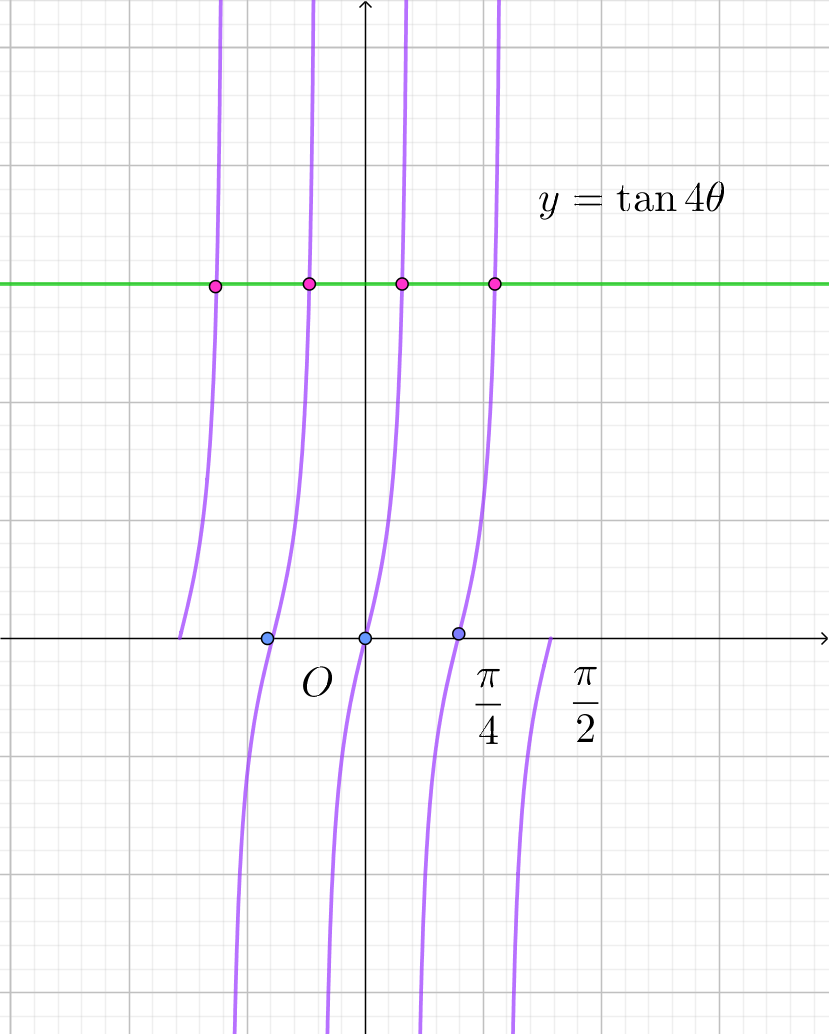

$\quad 区間が \ \ -\cfrac{\pi}{2} < \theta < \cfrac{\pi}{2}\ \ で端点を含まないことから、$
(i)$\ \ a > 0 ,\ \ a < 0 \quad のときは交点の個数は、n\ 個であるから、実数解の個数も \ n\ 個である。$
(ii)$\ \ a = 0 \ \ のときは交点の個数は、n-1\ 個であるから、実数解の個数も \ n-1\ 個である。$
$(考察1) f_n(x)\ と \ g_n(x)\ の単独の漸化式を導くこと$
$\quad 問題文では \quad f_n(x)\ と \ g_n(x)\ の漸化式が$
$\qquad f_{n+1}(x)=f_n(x)+xg_n(x) \hspace{10em}(1)$
$\qquad g_{n+1}(x)=g_n(x)-xf_n(x) \hspace{10em}(2)$
$とお互いの関係式で与えられていますので、単独の漸化式を導きます。$
$\quad (1)より \qquad xg_n=f_{n+1}-f_n \hspace{10em}(3)$
$\quad n \longrightarrow n+1 \quad とおいて \quad xg_{n+1}=f_{n+2}-f_{n+1} \hspace{2em}(4)$
$\quad (2)の両辺に \ x\ をかけて \qquad xg_{n+1}=xg_n -x^2f_n $
$\quad (3)(4)を代入して$
$\quad f_{n+2}-f_{n+1}=(f_{n+1}-f_n)-x^2f_n$
$\quad \therefore \ \ f_{n+2}-2f_{n+1}+(x^2+1)f_n=0$
$全く同様にして \qquad g_{n+2}-2g_{n+1}+(x^2+1)g_n=0$
$これで、f_n \ \ と \ \ g_n \ \ はともに同じ漸化式$
$\qquad F_{n+2}-2F_{n+1}+(x^2+1)F_n=0 \quad をみたすことがわかりました。$
$出発点(初期値)の違いだけなわけです。$
$(考察2) 問題(2)をf_n(x)とg_n(x)の定義式としてこれから問題文と問題(1)を導くこと$
$\quad 正の整数 \ n\ に対して、\sin n\theta =f_n(\tan \theta)\cos ^n\theta ,\qquad \cos n\theta =g_n(\tan \theta)\cos ^n\theta $
$\quad をみたす多項式を \ \ f_n(x),\ \ g_n(x)\ \ とする。$
(i)$\ \ 問題文の漸化式を導くこと$
$\quad n=1 \ \ のとき$
$\qquad \sin \theta=\tan \theta \cos \theta \quad だから \quad f_1(x)=x $
$\qquad \cos \theta =1 \times \cos \theta \quad だから \quad g_1(x)=1$
$\quad n=2 \ \ のとき$
$\qquad \sin 2\theta=2\sin \theta \cos \theta =2\tan \theta \cos ^2\theta \quad だから \quad f_2(x)=2x$
$\qquad \cos 2\theta =\cos ^2 \theta -\sin ^2 \theta =\cos ^2 \theta-\tan ^2\theta \cos ^2 \theta =(1-\tan ^2\theta)\cos ^2\theta \quad だから \quad g_2(x)=1-x^2$
$一般に$
\begin{eqnarray*} \sin (n+1)\theta &=&\sin n\theta \cos \theta +\cos n\theta\sin \theta\\ &=&f_n(\tan \theta)\cos ^{n+1}\theta +g_n(\tan \theta)\cos ^n\theta \sin \theta\\ &=&\{f_n(\tan \theta) +\tan \theta g_n(\tan \theta)\} \cos ^{n+1}\theta \\ \end{eqnarray*} $\quad したがって \quad f_{n+1}(\tan \theta)\cos ^{n+1}\theta =\{f_n(\tan \theta) +\tan \theta g_n(\tan \theta)\} \cos ^{n+1}\theta $
$\qquad \therefore \ \ f_{n+1}(x)=f_n(x) + xg_n(x)$
\begin{eqnarray*} \cos (n+1)\theta &=&\cos n\theta \cos \theta -\sin n\theta\sin \theta\\ &=&g_n(\tan \theta)\cos ^{n+1}\theta -f_n(\tan \theta)\cos ^n\theta \sin \theta\\ &=&\{g_n(\tan \theta) - \tan \theta f_n(\tan \theta)\} \cos ^{n+1}\theta \\ \end{eqnarray*} $\quad したがって \quad g_{n+1}(\tan \theta)\cos ^{n+1}\theta =\{g_n(\tan \theta) -\tan \theta f_n(\tan \theta)\} \cos ^{n+1}\theta $
$\qquad \therefore \ \ g_{n+1}(x)=g_n(x) - xf_n(x)$
$これで、問題文の漸化式が導けました。$
(ii)$\ \ 問題(1)の関係式を導くこと$
$\quad \sin n\theta =f_n(\tan \theta)\cos ^n\theta $
$\quad \cos n\theta =g_n(\tan \theta)\cos ^n\theta $
$\quad x=\tan \theta ,\qquad f_n(x)=\cfrac{\sin n\theta}{\cos ^n \theta},\qquad g_n(x)=\cfrac{\cos n\theta}{\cos ^n \theta} \quad より$
\begin{eqnarray*} f_n'(x) &=&\cfrac{d}{d\theta}\cfrac{\sin n\theta}{\cos ^n \theta} \cdot \cfrac{d\theta}{dx}\\ &=&\cfrac{n\cos n\theta\cos ^n\theta +\sin n\theta n\cos ^{n-1}\theta \sin \theta}{\cos ^{2n}\theta} \cdot \cfrac{1}{\cfrac{1}{\cos ^2\theta}}\\ &=&\cfrac{n\cos n\theta\cos ^n\theta +n\sin n\theta \cos ^{n-1}\theta \sin \theta}{\cos ^{2n}\theta} \cdot \cos ^2\theta\\ &=&\cfrac{n\cos n\theta\cos \theta +n\sin n\theta \sin \theta}{\cos ^{n-1}\theta} \\ &=&\cfrac{n\cos (n\theta - \theta)}{\cos ^{n-1}\theta} \\ &=&\cfrac{n\cos (n-1) \theta }{\cos ^{n-1}\theta} \\ &=&ng_{n-1}(x)\\ \end{eqnarray*} $\quad n \longrightarrow n+1 \ \ とおいて \quad f_{n+1}'(x)=(n+1)g_n(x)$
$\quad 全く同様にして \qquad g_{n+1}'(x)=-(n+1)f_n(x) \quad が導けます。$
$(考察3) f_n(x)\ と \ g_n(x)\ のみたす微分方程式を導くこと$
$\quad f_{n+1}=f_n + xg_n \hspace{15em}(1)$
$\quad g_{n+1}=g_n - xf_n \hspace{15em}(2)$
$\quad f_{n+1}'=(n+1)g_n \hspace{15em}(3)$
$\quad g_{n+1}'=-(n+1)f_n \hspace{14em}(4)$
$(2)を微分して \qquad g_{n+1}'=g_n' - f_n-xf_n'$
$(4)を代入して \qquad -(n+1)f_n=g_n' - f_n-xf_n'$
$\qquad g_n'=-nf_n+xf_n' \hspace{15em}(5)$
$これをもう一度微分して$
$\qquad g_n''=-nf_n'+f_n'+xf_n''=-(n-1)f_n'+xf_n'' \hspace{3em}(6)$
$(1)を微分して \qquad f_{n+1}'=f_n' + g_n +xg_n'$
$(3)を代入して \qquad (n+1)g_n=f_n' + g_n +xg_n'$
$\qquad ng_n=f_n'+xgn' $
$これをもう一度微分して$
$\qquad ng_n'=f_n''+g_n'' + xg_n' $
$\qquad (n-1)g_n'=f_n''+xg_n''$
$(5),(6)を代入して$
$\qquad (n-1)(-nf_n+xf_n')=f_n''+x\{-(n-1)f_n'+xf_n''\}$
$\qquad (x^2+1)f_n''-2(n-1)xf_n'+n(n-1)f_n=0$
$これが \ \ f_n(x)\ \ のみたす微分方程式です。$
$全く同様にして \ \ g_n(x)\ \ のみたす微分方程式$
$\qquad (x^2+1)g_n''-2(n-1)xg_n'+n(n-1)g_n=0$
$が得えられますが、f_n(x)\ \ も \ \ g_n(x)\ \ も同じ微分方程式になります。$
$(参考)$
$\cos n\theta \ \ を加法定理を用いて展開すると、\cos \theta\ \ の \ n\ 次多項式であらわされます。$
$そこで、x=\cos \theta \ \ とおいた多項式 \ \ T_n(x)\ \ を第 \ 1\ 種チェビシェフの多項式といいます。$
$すなわち \quad \cos n\theta =T_n(\cos \theta)$
$また、\sin n\theta=\sin \theta \times (\cos \theta の \ n-1\ 次多項式) \quad となりますので$
$\sin n\theta =\sin \theta S_{n-1}(\cos \theta) \quad とおいた \ \ S_n(x)\ \ を第 \ 2\ 種チェビシェフの多項式といいます。$
$このことについては後日詳しく述べる予定です。$
メインメニュー に戻る