MY MATH NOTE

千葉大学(理系) 2021年　問題5

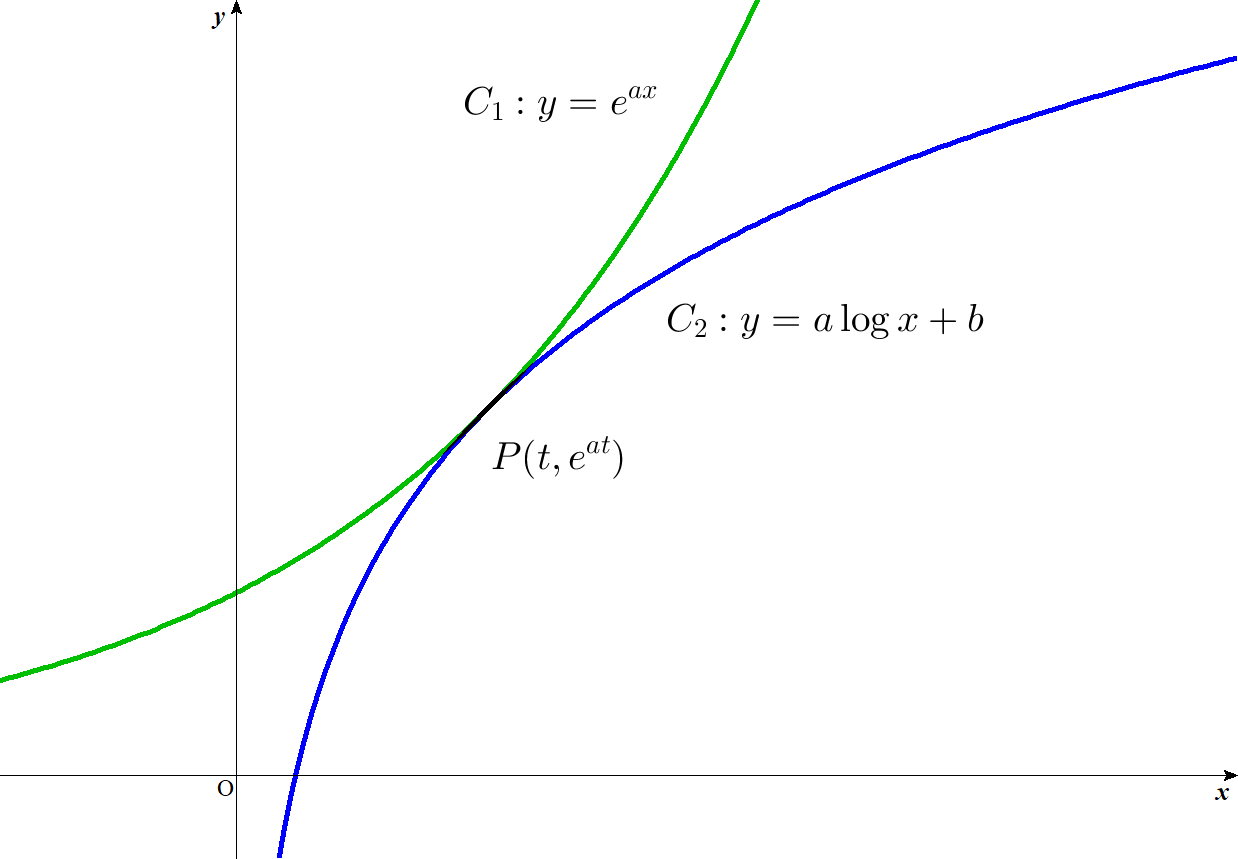
$2\ 曲線 \ C_1:y=e^{ax},\ \ C_2 : y=a\log x +b \ \ は、x\ 座標が \ t\ (0 < t <1)\ の点で接していて、a \ne 0 \ \ であるとする。$
$ただし、2\ 曲線が点 \ P\ で接するとは、P\ を共有し、P\ における接線が一致することである。$
$\qquad (1)\ \ a\ および \ b\ を \ t\ の式で表せ。$
\[(2)\ \ 曲線 \ C_1\ と \ x\ 軸、y\ 軸および直線 \ x=t \ で囲まれた部分の面積を \ S_1(t)\ とする。\] \[\quad 極限値 \ \ \lim _{t \rightarrow 1-0}S_1(t)\ \ を求めよ。\] \[(3)\ \ 曲線 \ C_2\ と \ x\ 軸、および直線 \ x=t\ で囲まれた部分の面積を \ S_2(t)\ とする。\] \[\quad 極限値 \ \ \lim _{t \rightarrow 1-0}S_2(t)\ \ を求めよ。\]

(1)

　
$\quad ②より \quad e^{at}=\cfrac{1}{t} \qquad at=\log \cfrac{1}{t}=-\log t$

$\quad \therefore \ \ a=-\cfrac{\log t}{t}$

$ここで、0 < t < 1 \quad だから \quad \log t < 0 \quad したがって \quad a > 0$

$グラフは右のとおり$

$\quad ①に代入して \quad b=e^{at}-a\log t=\cfrac{1}{t}+\cfrac{(\log t)^2}{t}$

(2)

　
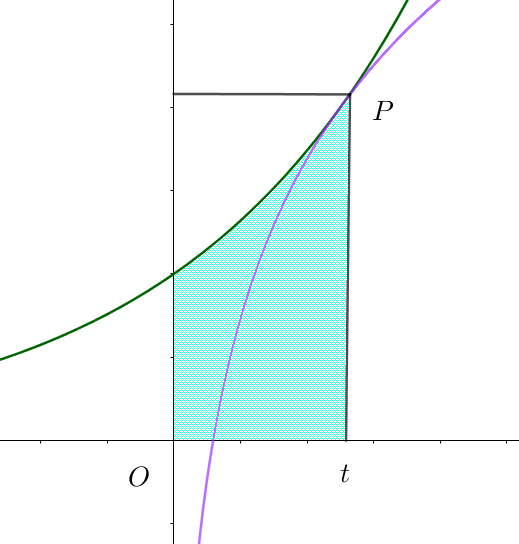
\[S_1(t)=\int _0^t e^{ax}dx=\cfrac{1}{a}\big[e^{ax}\big]_0^t=\cfrac{1}{a}\big(e^{at}-1\big)\] \begin{eqnarray*} \lim _{t \rightarrow 1-0}S_1(t) &=&\lim _{t \rightarrow 1-0}\cfrac{e^{at}-1}{a}\\ &=&\lim _{t \rightarrow 1-0}\cfrac{\dfrac{1}{t}-1}{-\dfrac{\log t}{t}}\\ &=&\lim _{t \rightarrow 1-0}\cfrac{t-1}{\log t}\\ &=&\lim _{t \rightarrow 1-0}\cfrac{1}{\dfrac{\log t-\log 1}{t-1}}\\ \end{eqnarray*} $\quad 分母は \ \ t=1 \ \ における \ \ \log t \ \ の微分係数だから \quad 1$
\[よって \quad \lim _{t \rightarrow 1-0}S_1(t)=\lim _{t \rightarrow 1-0}\cfrac{1}{\dfrac{\log t-\log 1}{t-1}}=1\]

(3)

　
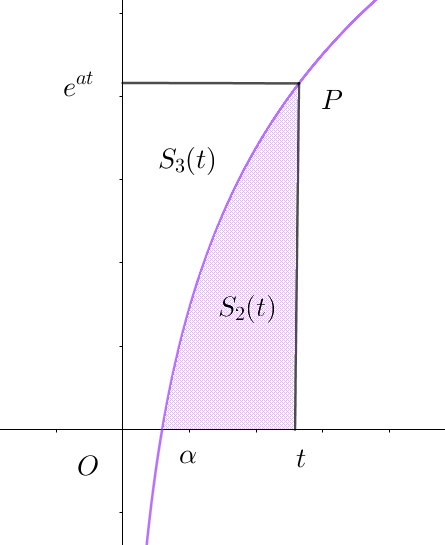
$\quad y=a\log x +b \quad が \ x\ 軸と交わる点を \ (\alpha,\ 0)\ とすると$

$\quad a\log \alpha +b=0 \quad より \quad \log \alpha =-\cfrac{b}{a} \qquad \alpha =e^{\scriptsize{-\cfrac{b}{a}}}$

$また、(1)より \quad a=-\cfrac{\log t}{t},\quad b=\cfrac{1}{t}+\cfrac{(\log t)^2}{t} \quad だから$

$\quad \cfrac{b}{a}=\cfrac{\dfrac{1}{t}+\cfrac{(\log t)^2}{t}}{ -\cfrac{\log t}{t}}=-\cfrac{1+(\log t)^2}{\log t}=-\log t -\cfrac{1}{\log t}$

$よって \quad \alpha =e^{\scriptsize{-\cfrac{b}{a}}}=e^{\log t +\scriptsize{\cfrac{1}{\log t}}}=e^{\log t}e^{\scriptsize{\cfrac{1}{\log t}}}=t\ e^{\scriptsize{\cfrac{1}{\log t}}}$

$\quad y=a\log x +b \quad を \ x\ について解くと \quad x=e^{\scriptsize{\cfrac{y-b}{a}}} \quad だから 右図の領域の面積を \ S_3(t)\ とおくと$
\begin{eqnarray*} S_3(t) &=&\int _0^{e^{at}} e^{\scriptsize{\cfrac{y-b}{a}}}dy\\ &=&\big[ae^{\scriptsize{\cfrac{y-b}{a}}}\big]_0^{e^{at}}\\ \\ &=&a\big(e^{\scriptsize{\cfrac{e^{at}-b}{a}}} -e^{\scriptsize{-\cfrac{b}{a}}}\big)\\ \\ &=&a\big(e^{\log t} -\alpha \big)\\ \\ &=&a(t -\alpha)\\ \end{eqnarray*}
\begin{eqnarray*} S_2(t) &=&te^{at} - S_3\\ \\ &=&1- a(t -\alpha)\\ &=&1 + \cfrac{\log t}{t}\big(t -te^{\scriptsize{\dfrac{1}{\log t}}}\big)\\ &=&1 + \log t \cdot \big(1 -e^{\scriptsize{\cfrac{1}{\log t}}}\big)\\ \end{eqnarray*}
$\qquad t \longrightarrow 1-0 \quad のとき \quad \log t \longrightarrow 0-0 \quad だから \quad \cfrac{1}{\log t} \longrightarrow -\infty \quad よって \quad e^{\scriptsize{\cfrac{1}{\log t}}} \longrightarrow 0$

\[したがって \quad \lim _{t \rightarrow 1-0}S_2(t)=1 + 0 \times 1=1\]

ページの先頭へ↑