MY MATH NOTE

千葉大学(理系) 2021年　問題3

$座標平面上に曲線 \ C \ :\ y=\cfrac{1}{x}\ \ および \ 3\ 点 \ A(-1,\ -1),\ B(-1,\ 0),\ D(1,\ 0)\ がある。曲線 \ C\ 上の点 \ P(t,\ \cfrac{1}{t})\ に$
$対して直線 \ AP\ と直線 \ y=-2\ の交点を \ Q\ とする。ただし、P\ が \ A\ と等しいとき、直線 \ AP\ とは \ A\ における$
$C\ の接線のこととする。また、直線 \ BQ\ に点 \ D\ から下ろした垂線と直線 \ BQ\ の交点を \ R\ とする。$
$(1)\ \ 点 \ P\ が曲線 \ C\ 上を動くとき、点 \ R\ の軌跡を求めよ。$
問題文が長いので、点の座標や直線の方程式を一つずつ求めていきましょう。点Rの座標は特徴ある分数式です。平方の和をとります。$
$(2)\ \ 直線 \ PR\ が原点を通るような実数 \ t\ の個数を求めよ。$

(1)

　
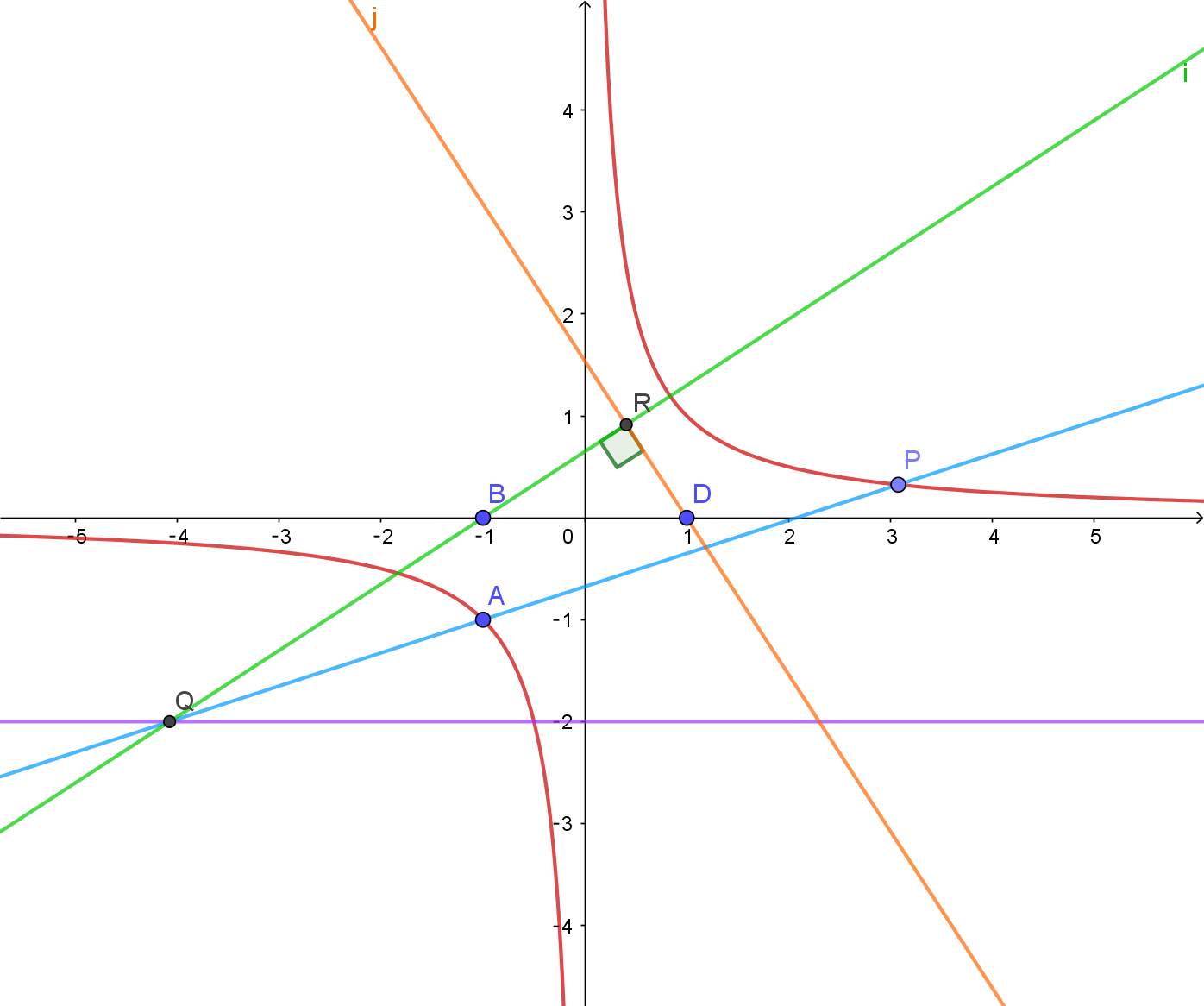
$右は点Pが第1象限にある場合のグラフです。$

$直線APの方程式は$

$\quad y=\cfrac{\dfrac{1}{t}+1}{t+1}(x+1)-1=\cfrac{1}{t}(x+1)-1$

$直線 \ AP\ と \ y=-2 \ との交点は$

$\quad -2=\cfrac{1}{t}(x+1)-1 \quad より \quad x=-t-1 \qquad \therefore \ \ Q(-t-1,\ -2)$

$直線 \ BQ\ の傾きを \ m\ とすると \qquad m=\cfrac{-2}{(-t-1)+1}=\cfrac{2}{t}$

$\quad 直線 \ BQ\ の方程式は \qquad y=\cfrac{2}{t}(x+1) \hspace{11em}①$

$\quad 直線 \ DR\ の傾きは \qquad -\cfrac{t}{2}$

$\quad 直線 \ DR\ の方程式は \qquad y=-\cfrac{t}{2}(x-1)　\hspace{10em}②$

$交点 \ R\ の座標は①、②を解いて \quad \cfrac{2}{t}(x+1)=-\cfrac{t}{2}(x-1) \qquad (t^2+4)x=t^2-4 \qquad \therefore \ \ x=\cfrac{t^2-4}{t^2+4}$

$②に代入して \quad y=-\cfrac{t}{2}\big(\cfrac{t^2-4}{t^2+4}-1 \big)=\cfrac{4t}{t^2+4}$

　
$\quad \therefore \ \ R\ (\cfrac{t^2-4}{t^2+4},\ \cfrac{4t}{t^2+4})$

$\qquad x^2+y^2=\big(\cfrac{t^2-4}{t^2+4}\big)^2+\big(\cfrac{4t}{t^2+4}\big)^2=\cfrac{(t^2+4)^2}{(t^2+4)^2}=1$

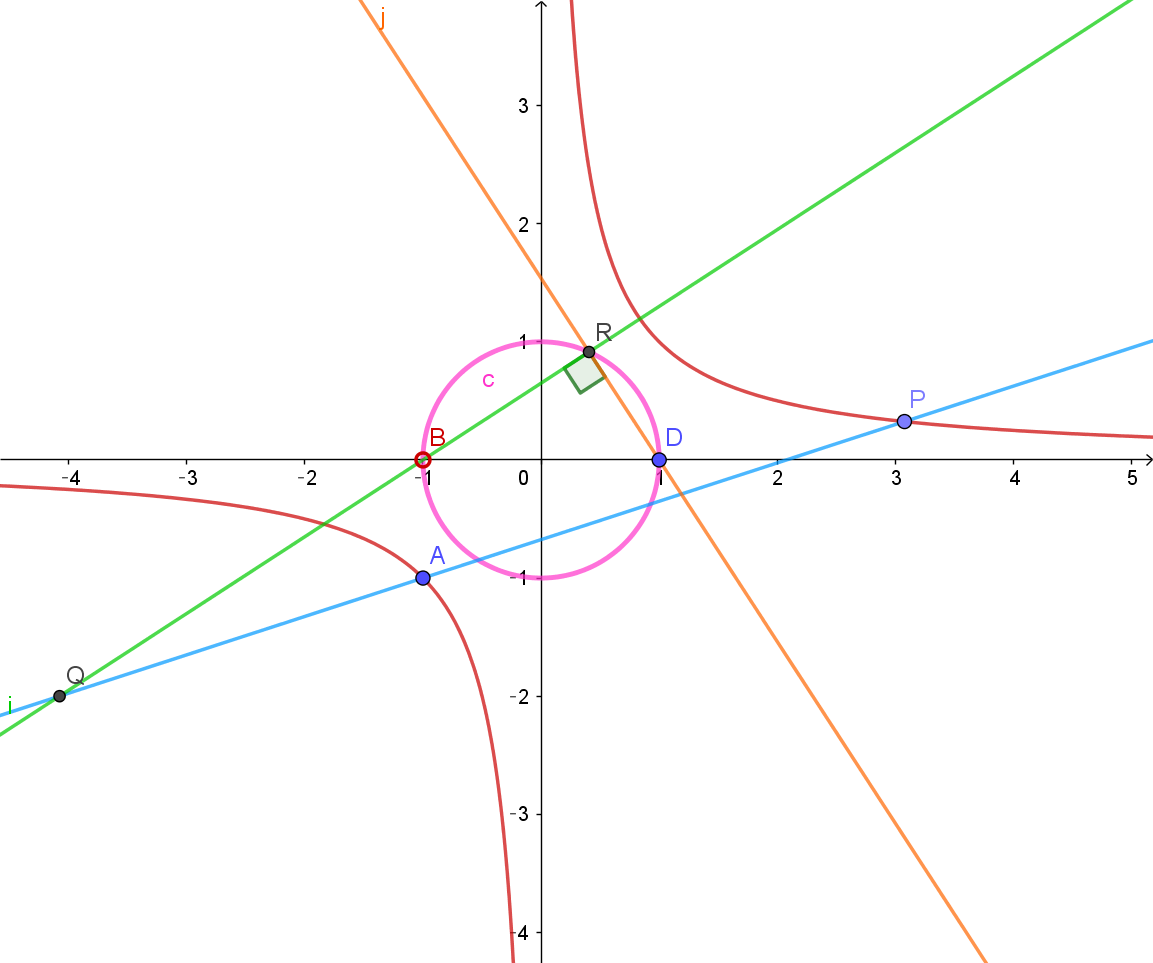
$よって、点 \ R\ の軌跡は、原点中心、半径 \ 1\ の円$

$ ただし、t \ne 0 \quad だから \quad 点 \ B\ (-1,\ 0)\ \ を除く。$

$グラフは右図のとおり$

(2)

　
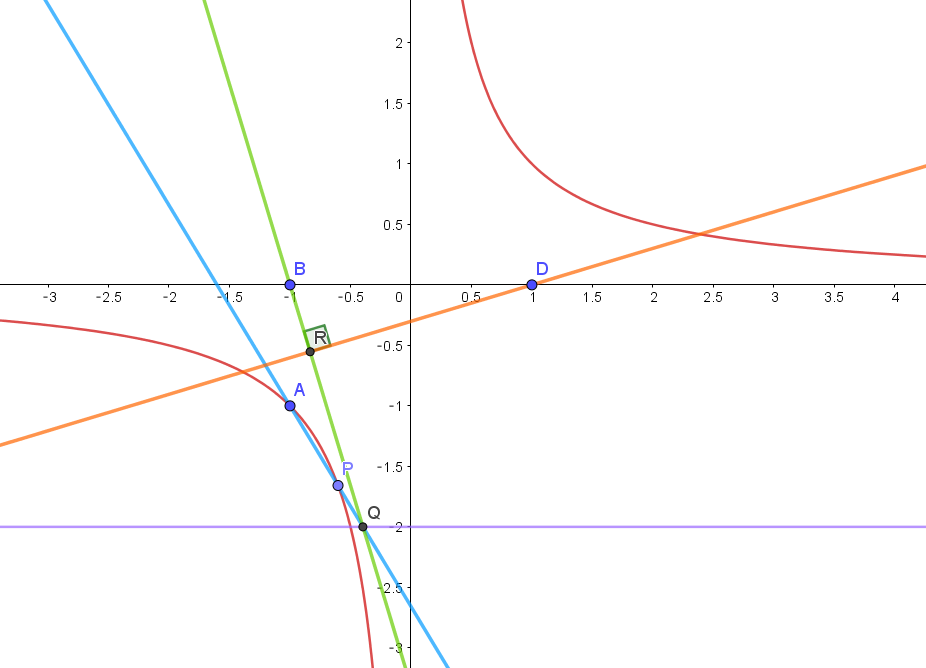
$右は点 \ P\ が第 \ 3\ 象限にある場合のグラフです。$

$\quad P(t,\ \cfrac{1}{t}),\quad R(\cfrac{t^2-4}{t^2+4},\ \cfrac{4t}{t^2+4})\quad だから $

$直線PRの傾き \ n\ は$
\begin{eqnarray*} n &=&\cfrac{\dfrac{4t}{t^2+4}-\dfrac{1}{t}}{\dfrac{t^2-4}{t^2+4}-t}\\ \\ &=&\cfrac{4t^2-(t^2+4)}{t(t^2-4)-t^2(t^2+4)}\\ \\ &=&-\cfrac{3t^2-4}{t^4-t^3+4t^2+4t} \end{eqnarray*}
$直線PRの方程式は$
\begin{eqnarray*} y &=&n(x-t)+\cfrac{1}{t}\\ \\ &=&nx+\cfrac{3t^2-4}{t^3-t^2+4t+4}+\cfrac{1}{t}\\ \\ &=&nx+\cfrac{4t^3-t^2+4}{t(t^3-t^2+4t+4)}\\ \end{eqnarray*} $原点を通るから \qquad \cfrac{4t^3-t^2+4}{t(t^3-t^2+4t+4)}=0$

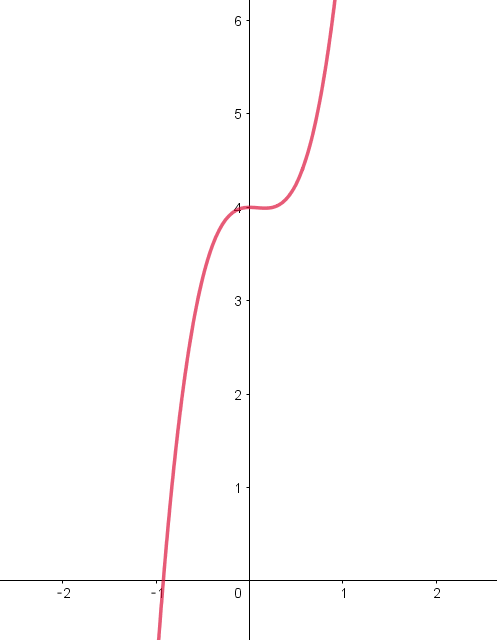
$f(t)=4t^3-t^2+4 \quad とおくと \quad f'(t)=12t^2-2t=2t(6t-1)$

$f(t)\ の増減表は$

　
\[ \begin{array}{c||c|c|c|c|c} \hline t & \cdots & 0 & \cdots & \cfrac{1}{6} & \cdots \\ \hline f'(t)& + & 0 & - & 0 & + \\ \hline f(t) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \hline \end{array} \] $\qquad t=0\ で極大となり、極大値は \quad f(0)=4$

$\qquad t=\cfrac{1}{6} \ で極小となり、極小値は \quad f(\cfrac{1}{6})=\cfrac{4}{6^3}-\cfrac{1}{6^2}+4 > 0$

$f(-1)=-1 \quad だから、中間値の定理より \quad f(\alpha)=0 \ \ となる \ \alpha \ が$
$区間 \ (-1,\ 0)\ に存在する。$
$f(t)\ はこの区間で単調増加であるからただ \ 1\ つである。$

$このとき、f(\alpha)=4\alpha ^3 -\alpha ^2 +4=0 \quad より \quad \alpha ^3=\cfrac{\alpha ^2}{4}-1 $

$直線 \ PR\ の方程式の \ y\ 切片(定数項)の分母の \ 3\ 次式に \ \alpha \ を代入すると$

$\quad \alpha ^3- \alpha ^2+ 4\alpha + 4=\big(\cfrac{\alpha ^2}{4}-1\big)- \alpha ^2+ 4 \alpha +4=-\cfrac{3}{4} \alpha ^2+ 4\alpha +3=-\cfrac{1}{4}(\alpha -6)(3\alpha +2)$

$明らかに \quad \alpha \ne 6,\quad \alpha \ne -\cfrac{2}{3} \quad より \quad \alpha ^3 - \alpha ^2+ 4\alpha + 4 \ne 0 $

$また　\alpha \ne 0 \quad だから \quad 直線 \ PR\ の\ y\ 切片(定数項)の分母 \ \ne 0$

$したがって、 直線\ PR\ が原点を通るような実数 \ t\ の個数は \ 1\ 個である。$

ページの先頭へ↑