千葉大学(理系) 2025年　問題8


$正方形に対して、その \ 2\ 本の対角線の交点を、その正方形の中心と呼ぶ。また、すべての内角が \ 180°未満の$
$四角形を凸四角形と呼ぶ。このとき、以下の問いに答えよ。$
$(1)\ \ 複素数平面上に正方形PQRS \ があり、その中心 \ T\ から見て \ 4\ 点P,\ Q,\ R,\ S\ は反時計回りに並んでいる。$
$\quad 頂点P,\ Q\ の座標を表す複素数を \ p,\ q\ とするとき、中心T\ の座標を表す複素数 \ t\ を \ p,\ q\ を用いて表せ。$
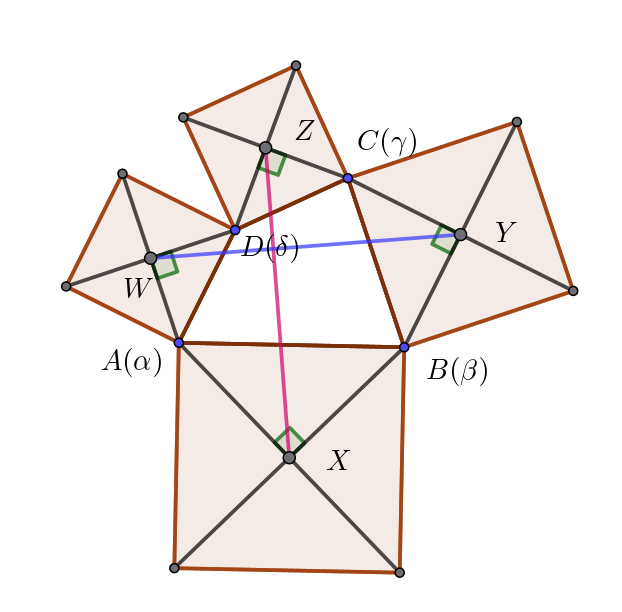
$(2)\ \ 複素数平面上に凸四角形ABCD\ がある。頂点A,\ B,\ C,\ D\ の座標を表す複素数をそれぞれ \ \alpha,\ \beta,\ \gamma,\ \delta \ \ と$
$\quad する。四角形ABCD\ の外側に線分AB\ を \ 1\ 辺とする正方形を描きその中心を \ X\ とする。同様に、ABCD\ の$
$\quad 外側に線分BC\ を \ 1\ 辺とする正方形を描きその中心を \ Y\ とし、ABCD\ の外側に線分CD\ を \ 1\ 辺とする正方$
$\quad 形を描きその中心を \ Z\ とし、ABCD\ の外側に線分DA\ を \ 1\ 辺とする正方形を描きその中心を \ W\ とする。$
$\quad このとき、XZ=YW \ \ であり、かつ、直線XZ\ と直線YW\ が直交することを証明せよ。$
$(3)\ \ (2)において、線分XZ\ と線分YW\ がそれらの中点で交わるとき、四角形ABCD\ はどのような四角形に$
$\quad なるか、理由とともに述べよ。$


(1)

　

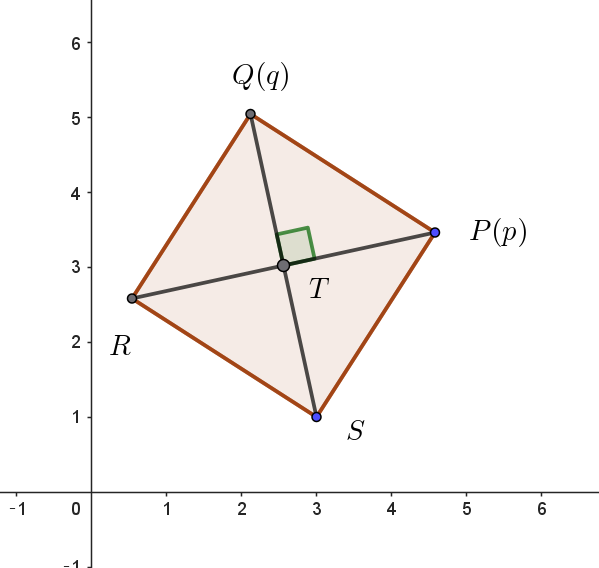
$\vec{TQ}\ は \ \vec{TP}\ を \ T\ の周りに \ \ \dfrac{\pi}{2}\ \ 回転したものだから$

$q-t=(p-t)i$

$(1-i)t=q-pi$

$t=\dfrac{q-pi}{1-i}=\dfrac{1}{2}(q-pi)(1+i)=\dfrac{1}{2}(q+p+i(q-p))$


(2)


$中心 \ X,\ Y,\ Z,\ W\ の座標を表す複素数をそれぞれ \ x,\ y,\ z,\ w \ \ とする。$

$(1) より$

$x=\dfrac{1}{2}(\alpha + \beta +i(\alpha - \beta)),\quad y=\dfrac{1}{2}(\beta + \gamma +i(\beta - \gamma)),\quad z=\dfrac{1}{2}(\gamma + \delta +i(\gamma - \delta)),\quad w=\dfrac{1}{2}(\delta + \alpha +i(\delta - \alpha))$

　

$このとき$
\begin{eqnarray*} XZ^2 &=&|z-x|^2\\ \\ &=&\big|\dfrac{1}{2}(\gamma + \delta +i(\gamma - \delta)) -\dfrac{1}{2}(\alpha + \beta +i(\alpha - \beta))\big|^2\\ \\ &=&\dfrac{1}{4}|(\gamma + \delta -\alpha -\beta )+i(\gamma - \delta -\alpha + \beta )|^2\\ \\ &=&\dfrac{1}{4}|(\gamma - \alpha) +(\delta -\beta ))+ i((\gamma - \alpha )-(\delta - \beta) )|^2\\ \\ &=&\dfrac{1}{4}\{((\gamma - \alpha) + (\delta -\beta) )^2+ ((\gamma - \alpha )-(\delta - \beta) )^2\}\\ \\ &=&\dfrac{1}{2}\{(\gamma - \alpha)^2 + (\delta -\beta)^2\} \\ \end{eqnarray*}
\begin{eqnarray*} YW^2 &=&|w - y|^2\\ \\ &=&\big|\dfrac{1}{2}(\delta + \alpha +i(\delta - \alpha)) -\dfrac{1}{2}(\beta + \gamma +i(\beta - \gamma))\big|^2\\ \\ &=&\dfrac{1}{4}|(\delta + \alpha -\beta -\gamma )+i(\delta - \alpha -\beta + \gamma )|^2\\ \\ &=&\dfrac{1}{4}|((\delta - \beta) -(\gamma -\alpha )+i((\delta - \beta) + (\gamma - \alpha))|^2\\ \\ &=&\dfrac{1}{4}\{((\delta - \beta) - (\gamma -\alpha) )^2+ ((\delta - \beta ) +(\gamma - \alpha))^2\}\\ \\ &=&\dfrac{1}{2}\{(\delta - \beta )^2+ (\gamma -\alpha )^2 \\ \\ \end{eqnarray*} $よって \quad XZ^2=YW^2 \quad すなわち \quad XZ=YW$


$また、 \vec{XZ} 、\vec{YW}\ \ の表す複素数をそれぞれ \ \varepsilon ,\ \zeta \ \ とおくと$
\begin{eqnarray*} \varepsilon &=&z-x\\ \\ &=&\dfrac{1}{2}(\gamma + \delta +i(\gamma - \delta)) - \dfrac{1}{2}(\alpha + \beta +i(\alpha - \beta))\\ \\ &=&\dfrac{1}{2}(\gamma + \delta - \alpha - \beta +i(\gamma - \delta -\alpha +\beta))\\ \end{eqnarray*}
\begin{eqnarray*} \zeta &=&w-y\\ \\ &=&\dfrac{1}{2}(\delta + \alpha +i(\delta - \alpha))- \dfrac{1}{2}(\beta + \gamma +i(\beta - \gamma))\\ \\ &=&\dfrac{1}{2}(\delta + \alpha - \beta - \gamma +i(\delta - \alpha -\beta +\gamma))\\ \end{eqnarray*}
\begin{eqnarray*} i\varepsilon &=&i \times \dfrac{1}{2}(\gamma + \delta - \alpha - \beta +i(\gamma - \delta -\alpha +\beta))\\ \\ &=&\dfrac{1}{2}(-(\gamma - \delta -\alpha +\beta) +i(\gamma + \delta - \alpha - \beta ))\\ \\ &=&\dfrac{1}{2}(\delta + \alpha - \beta - \gamma +i(\delta - \alpha -\beta +\gamma))\\ \\ &=&\zeta \end{eqnarray*} $よって \quad \vec{XZ} \perp \vec{YW}$


(3)


$線分XZ\ と線分YW\ がそれらの中点で交わることを複素数で表すと$

$\dfrac{x+z}{2}=\dfrac{y+w}{2} \quad だから$

$\dfrac{1}{2}(\alpha + \beta +i(\alpha - \beta))+\dfrac{1}{2}(\gamma + \delta +i(\gamma - \delta))=\dfrac{1}{2}(\beta + \gamma +i(\beta - \gamma))+ \dfrac{1}{2}(\delta + \alpha +i(\delta - \alpha))$

　

$\beta - \alpha=\gamma -\delta $

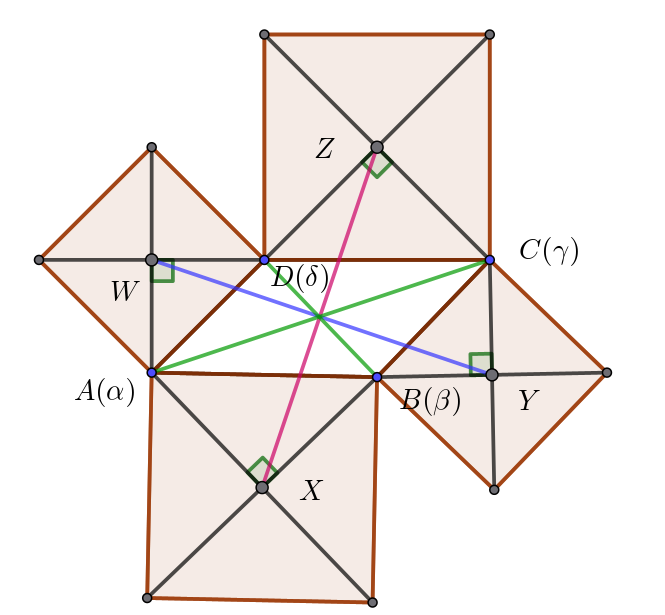
$これをベクトルで表すと \quad \vec{AB}=\vec{DC}$

$よって、四角形ABCD\ は平行四辺形$


ページの先頭へ↑




メインメニュー　に戻る