千葉大学(理系) 2025年　問題7


$すべての実数 \ x\ に対して定義された関数 \ \ f(x)=\dfrac{16-x^2}{\sqrt{x^4-2x^2+16}} \ \ について、以下の問いに答えよ。$
$(1)\ \ f'(x)=0 \ \ を満たす実数 \ x\ をすべて求めよ。$
$(2)\ \ f''(x)=0 \ \ を満たす実数 \ x\ をすべて求めよ。$
$(3)\ \ y=f(x)\ の凹凸、変曲点、ならびに漸近線を調べて、そのグラフの概形を描け。$
$(4)\ \ 点(0,\ t)\ から曲線 \ y=f(x) \ に接線が引けるような実数 \ t\ の範囲を求めよ。$


(1)


$f(x)=\dfrac{16-x^2}{\sqrt{x^4-2x^2+16}} \ \ より$

\begin{eqnarray*} f'(x) &=&\dfrac{-2x \sqrt{x^4-2x^2+16} -(16-x^2) \times \dfrac{2x^3-2x}{\sqrt{x^4-2x^2+16}}}{x^4-2x^2+16}\\ \\ &=&\dfrac{-2x (x^4-2x^2+16)-2(16-x^2)(x^3-x)}{(x^4-2x^2+16)^{\frac{3}{2}}}\\ \\ &=&-\dfrac{30x^3}{(x^4-2x^2+16)^{\frac{3}{2}}} \end{eqnarray*}
$f'(x)=0 \quad より \quad x=0$


(2)


$f'(x)=-30x^3(x^4-2x^2+16)^{-\frac{3}{2}} \quad より$
\begin{eqnarray*} f''(x) &=&-90x^2(x^4-2x^2+16)^{-\frac{3}{2}}+ 45x^3(x^4-2x^2+16)^{-\frac{5}{2}}(4x^3-4x)\\ \\ &=&\cfrac{-90x^2(x^4-2x^2+16) + 45x^3(4x^3-4x)}{(x^4-2x^2+16)^{-\frac{5}{2}}}\\ \\ &=&\cfrac{90x^2(x^4-16)}{(x^4-2x^2+16)^{-\frac{5}{2}}}\\ \\ &=&\cfrac{90x^2(x^2 +4)(x+2)(x-2)}{(x^4-2x^2+16)^{-\frac{5}{2}}}\\ \end{eqnarray*}
$f''(x)=0 \quad より \quad x=0, \ \ x=\pm 2$


(3)


$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & -2 & \cdots & 0 & \cdots & 2 & \cdots \\ \hline f'(x) & + & + & + & 0 & - & - & -\\ \hline f''(x) & + & 0 & - & 0 & - & 0 & +\\ \hline f(x) & \nearrow & 変曲点 & \nearrow & 極大 & \searrow & 変曲点 & \searrow \\ & 下に凸 & & 上に凸 & & 上に凸 & & 下に凸\\ \end{array} \]

　

$f(\pm 2)=\dfrac{16-4}{\sqrt{16-8+16}}=\sqrt{6}$

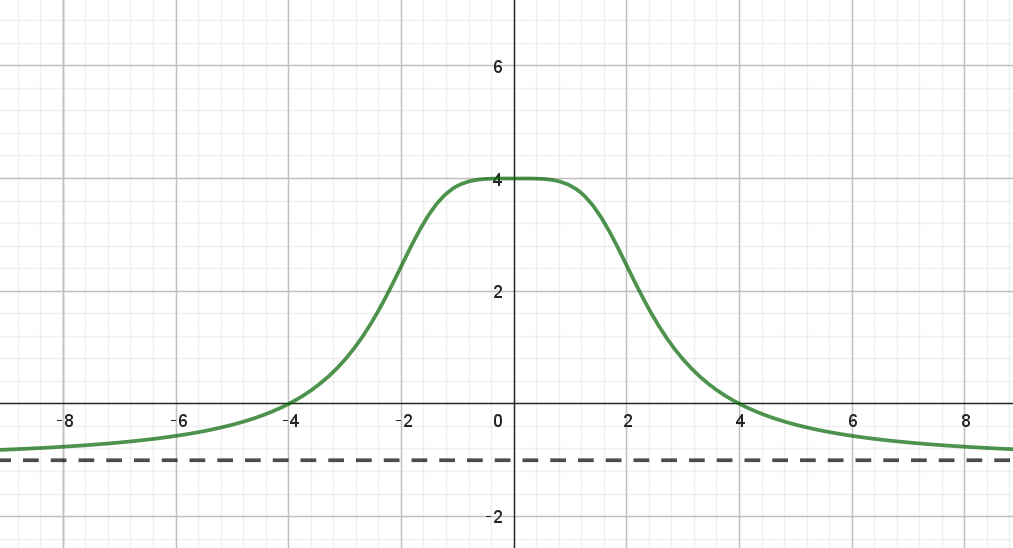
$変曲点は \ \ (-2,\ \sqrt{6}),\ \ (2,\ \sqrt{6})$

$x=0 \ \ のとき極大で、極大値は \ \ f(0)=\dfrac{16}{\sqrt{16}}=4$

$f(x)=\dfrac{16-x^2}{x^2\sqrt{1-\dfrac{2}{x^2} +\dfrac{16}{x^4}}} $

$x \longrightarrow \pm \infty \ \ のとき \ \ f(x) \longrightarrow -1 \quad だから \quad y=-1 \ \ は漸近線$

$なお、y=f(x)\ は偶関数だからグラフは \ y\ 軸について対称$

$グラフの概形は右図のとおり$


(4)

　

$曲線上の接点を \ (u,\ f(u)) \ \ とおくと$

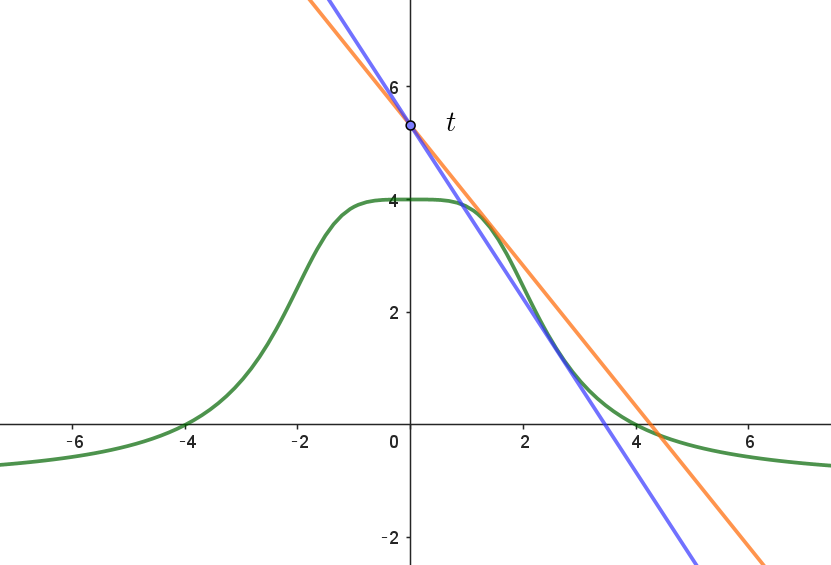
$この点における接線は$

$y=f'(u)(x-u)+f(u)$

$(0,\ t)\ \ を通るから$

$t=-uf'(u)+f(u)$

$これを満たす \ (u,\ t)\ が存在するかどうかは$

$g(u)=-uf'(u)+f(u) \quad とおき$

$y=t \ \ と \ \ y=g(u) \ \ のグラフの交点の数を調べればよい。$

$なお、f(u)\ は偶関数、f'(u)\ は奇関数だから$

$g(-u)=uf'(-u)+f(-u)=-uf'(u)+f(u)=g(u)$

$よって、g(u)\ は偶関数だからグラフは \ y\ 軸について対称$

\begin{eqnarray*} g'(u) &=&-f'(u)-uf''(u)+f'(u)\\ \\ &=&-uf''(u)\\ \\ &=&-\cfrac{90u^3(u^2 +4)(u+2)(u-2)}{(u^4-2u^2+16)^{-\frac{5}{2}}}\\ \end{eqnarray*} $増減表$
\[ \begin{array}{c||c|c|c|c|c} u& \cdots & -2 & \cdots & 0 & \cdots & 2 & \cdots \\ \hline g'(u) & + & 0 & - & 0 & + & 0 & -\\ \hline g(u) & \nearrow & 極大 & \searrow & 極小 & \nearrow & 極大 & \searrow \\ \end{array} \]
$u=0 \ \ のとき極小で、極小値 \ \ g(0)=4$

$u=\pm 2 \ \ のとき極大で、極大値 \ \ g(\pm 2)=\dfrac{2 \times 30 \times 2^3}{(16-2 \times 4 +16)^{\frac{3}{2}}}+\dfrac{16-4}{(16-2 \times 4+16)^{\frac{1}{2}}}=\dfrac{8\sqrt{6}}{3}$

$g(u)=-uf'(u)+f(u) \ \ において \quad u \longrightarrow \infty \quad とすると$

$uf'(u)=-\dfrac{30u^4}{(u^4-2u^2+16)^{\frac{3}{2}}}=-\dfrac{30u^4}{u^6((1-\dfrac{2}{u^2}+\dfrac{16}{u^4})^{\frac{3}{2}}}=-\dfrac{30}{u^2((1-\dfrac{2}{u^2}+\dfrac{16}{u^4})^{\frac{3}{2}}} \longrightarrow 0$

$(3)より \quad f(u) \longrightarrow -1 $

$したがって \quad g(u) \longrightarrow -1 \quad となって \quad y=-1\ \ は漸近線$

　

$y=g(u) \ のグラフは右図のとおり$

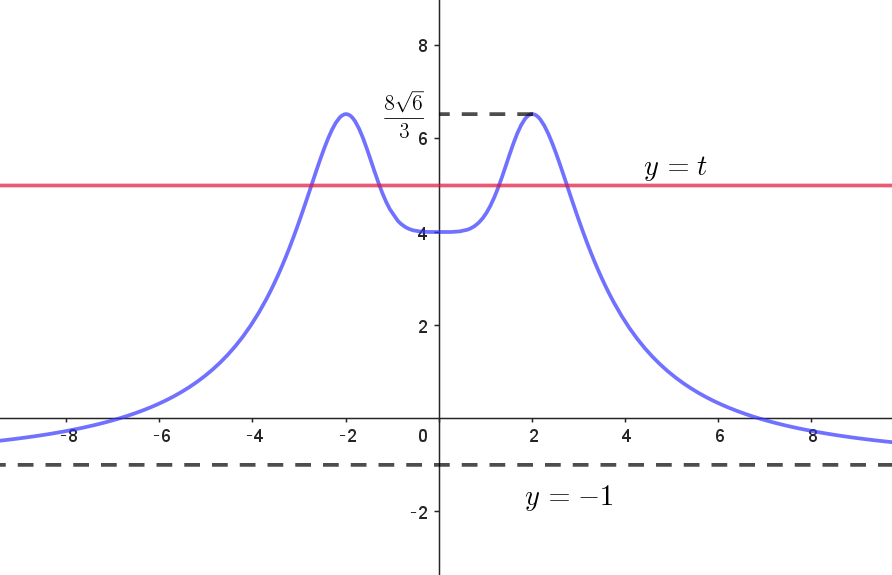
$したがって\ \ 点(0,\ t)\ から曲線 \ y=f(x) \ に$

$接線が引けるような実数 \ t\ の範囲は$

$y=t \ と \ y=g(u)\ のグラフが交点をもつ$

$場合だから \quad -1 < t \leqq \dfrac{8\sqrt{6}}{3} $


$なお、y=t \ と \ y=g(u)\ のグラフの交点の個数は$

(i)$\ \ t \leqq -1 \ \ のとき \hspace{3em}　0\ 個$

(ii)$\ \ -1 < t <4 \ \ のとき \ \ 　2\ 個$

(iii)$\ \ t=4 \ \ のとき \hspace{4em} 3\ 個$

(iv)$\ \ 4 < t < \dfrac{8\sqrt{6}}{3}\ \ のとき \quad 4\ 個$

(v)$ \ \ t = \dfrac{8\sqrt{6}}{3}\ \ のとき \hspace{3.5em} 2\ 個$

(vi)$\ \ t > \dfrac{8\sqrt{6}}{3} \ \ のとき \hspace{3em} 0\ 個$


ページの先頭へ↑




メインメニュー　に戻る