千葉大学(理系) 2025年　問題6


$座標平面上に、曲線 \ D:y=\log x \ \ (x > 0)\ \ とその上の点A(a,\ \log a) \ \ がある。半径 \ r\ の円C\ は \ y\ 軸に接し、$
$かつ、円C\ は曲線 \ D\ と点A\ で同一の接線を持つ。さらに、r < a \ \ が成り立つとする。このとき、以下の$
$問いに答えよ。$
$(1)\ \ r\ を \ a\ を用いて表せ。$
$(2)\ \ r > \dfrac{a}{2} \ \ となることを示せ。$
$(3)\ \ a=\sqrt{3}\ \ のとき、x\ 軸、y\ 軸、円C\ の下半分と曲線D\ によって囲まれる領域の面積を求めよ。$


(1)

　

$A(a,\ \log a) \ における接線と \ x\ 軸のなす角を \ \theta \ とすると$

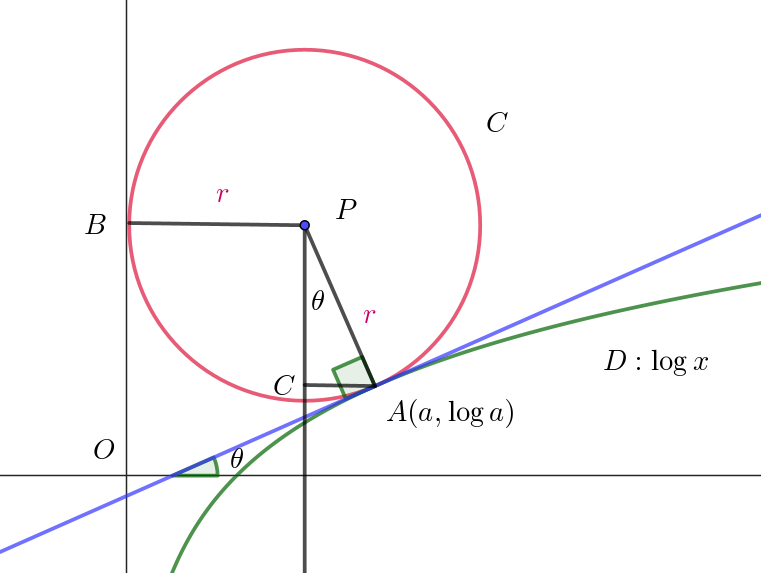
$y=\log x \ \ より \ \ y'=\dfrac{1}{x}\ \ だから$

$\dfrac{1}{a}=\tan \theta$

$\dfrac{1}{\sin ^2\theta}=1+\dfrac{1}{\tan ^2 \theta}=1+a^2$

$\sin \theta=\dfrac{1}{\sqrt{1+a^2}}$

$点A\ における円C\ の接線は、AP\ に垂直だから、\angle APC=\theta $

$BP+CA=a \ \ より \quad r+r\sin \theta =a$

$r(1+\sin \theta)=a$

\begin{eqnarray*} r &=&\dfrac{a}{1+\sin \theta}\\ \\ &=&\dfrac{a}{1+\dfrac{1}{\sqrt{1+a^2}}}\\ \\ &=&\dfrac{a\sqrt{1+a^2}}{\sqrt{1+a^2} +1}\\ \\ &=&\dfrac{a\sqrt{1+a^2}(\sqrt{1+a^2} -1)}{(1+a^2)-1}\\ \\ &=&\dfrac{\sqrt{1+a^2}(\sqrt{1+a^2} -1)}{a}\\ \\ &=&\dfrac{1+a^2-\sqrt{1+a^2}}{a}\\ \end{eqnarray*}

(2)


\begin{eqnarray*} & &r-\dfrac{a}{2}\\ \\ &=&\dfrac{1+a^2-\sqrt{1+a^2}}{a}-\dfrac{a}{2}\\ \\ &=&\dfrac{2+2a^2-2\sqrt{1+a^2}-a^2}{2a}\\ \\ &=&\dfrac{a^2-2\sqrt{1+a^2}+2}{2a}\\ \\ &=&\dfrac{(a^2+1)-2\sqrt{1+a^2}+1}{2a}\\ \\ &=&\dfrac{(\sqrt{1+a^2}-1)^2}{2a}\\ \\ &>&0 \end{eqnarray*} $よって \quad r > \dfrac{a}{2}$


(3)

　

$a=\sqrt{3} \ \ のとき (1)より \quad r=\dfrac{1+3-\sqrt{1+3}}{\sqrt{3}}=\dfrac{2}{\sqrt{3}}$

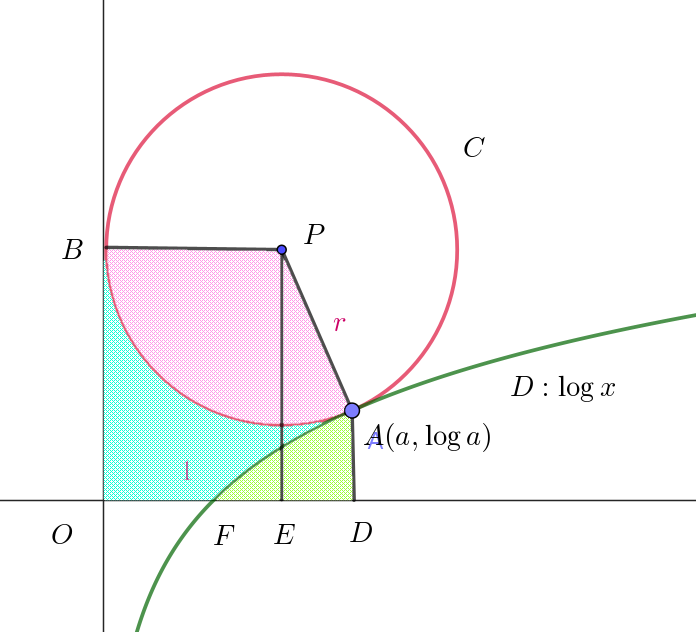
$(1)より \quad \sin \theta=\dfrac{1}{\sqrt{1+3}}=\dfrac{1}{2} \quad \therefore \ \ \theta=\dfrac{\pi}{6}$

$円C\ の中心P(b,\ c)\ は$

$b=r= \dfrac{2}{\sqrt{3}}$

$c=\log \sqrt{3}+r\cos \dfrac{\pi}{6}=\log \sqrt{3} + \dfrac{2}{\sqrt{3}} \times \dfrac{\sqrt{3}}{2}=1+ \log \sqrt{3}$

(i)$\ \ 長方形OEPB=\dfrac{2}{\sqrt{3}} \times (1+\log \sqrt{3})=\dfrac{2\sqrt{3}}{3}(1+\log \sqrt{3})$

(ii)$\ \ 台形APED= \dfrac{1}{2}(AD+PE) \times ED=\dfrac{1}{2}(\log \sqrt{3} + 1+\log \sqrt{3}) \times (\sqrt{3}-\dfrac{2}{\sqrt{3}})=\dfrac{\sqrt{3}}{6}(1+2\log \sqrt{3})$

(iii)$\ \ 扇形PBAの面積=\pi r^2 \times \dfrac{\frac{\pi}{2}+\frac{\pi}{6}}{2\pi}=\pi \times \dfrac{4}{3} \times \dfrac{1}{3}=\dfrac{4}{9}\pi$

(iv)$\ \ D:\log x \ \ と \ x\ 軸で囲まれた領域 \ G\ の面積は$

\[\quad G=\int_1^{\sqrt{3}} \log x dx=\big[x\log x -x\big]_1^{\sqrt{3}}=\sqrt{3}\log \sqrt{3}-\sqrt{3}+1=1-\sqrt{3}+ \sqrt{3}\log \sqrt{3}\]
$よって、求める領域の面積 \ S\ は$

\begin{eqnarray*} S &=&長方形OEPB ＋台形APED - 扇形PBA -G\\ \\ &=&\dfrac{2\sqrt{3}}{3}(1+\log \sqrt{3}) + \dfrac{\sqrt{3}}{6}(1+2\log \sqrt{3}) - \dfrac{4}{9}\pi - \big(1-\sqrt{3}+ \sqrt{3}\log \sqrt{3}\big)\\ \\ &=&-1+\dfrac{11\sqrt{3}}{6} - \dfrac{4}{9}\pi \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る