千葉大学(文系) 2025年 問題3
$座標平面上に \ 3\ 点A(0,\ 2),\ B(-\sqrt{3},\ -1),\ C(\sqrt{3},\ -1)\ があり、三角形ABC\ の内接円上に点P\ がある。$
$また、2\ 点D,\ E\ を \ \vec{PB}=\vec{AD},\ \ \vec{PO}=\vec{CE}\ \ となるようにとる。ここで \ O\ は原点(0,\ 0)\ である。このとき、$
$以下の問いに答えよ。$
$(1)\ \ 内積の値 \ \ \vec{PD}\cdot \vec{PE}\ \ が点P\ の位置によらず一定であることを示し、その値を求めよ。$
$(2)\ \ 線分DE\ の中点を \ M\ とする。点P\ が三角形ABC\ の内接円上を \ 1\ 周するとき、点M\ の軌跡を求めよ。$
(1)
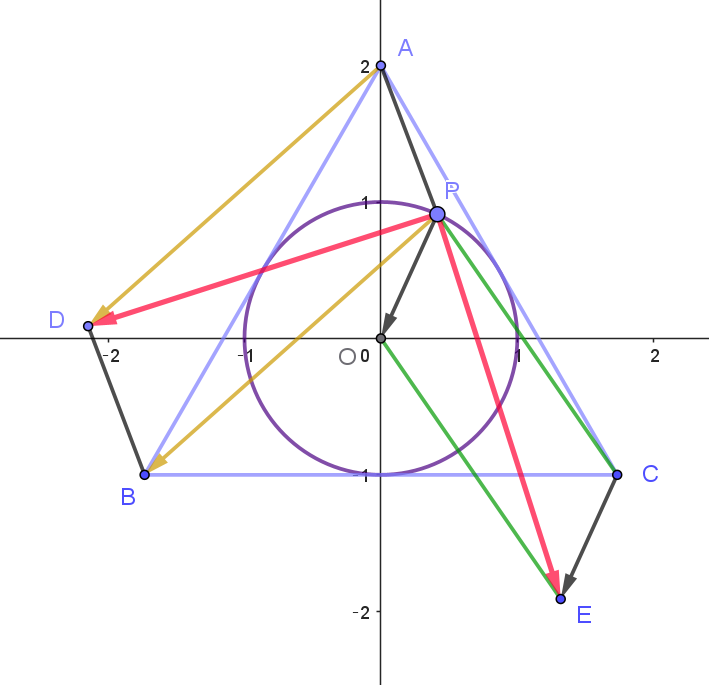
$AB^2=(-\sqrt{3})^2+(-1-2)^2=12$
$AC^2=(\sqrt{3})^2+(-1-2)^2=12$
$BC^2=(\sqrt{3}+\sqrt{3})^2=12$
$よって、三角形ABC\ は正三角形だから内心I\ と重心G\ は一致する。$
$G(x,y)は \quad x=\dfrac{0-\sqrt{3}+\sqrt{3}}{3}=0,\quad y=\dfrac{2-1-1}{3}=0$
$したがって 内心I\ の座標も I(0,\ 0)$
$内接円の半径 \ r\ は、内心I\ と辺BC\ の距離だから \quad r=1$
$よって、内接円上の任意の点P(a,\ b)\ は \quad a^2+b^2=1 \quad とおける。$
$四角形ADBP \ と \ OECP\ は平行四辺形だから$
\begin{eqnarray*} \vec{PD} &=&\vec{PA}+\vec{PB}\\ \\ &=&(\vec{OA}-\vec{OP})+(\vec{OB}-\vec{OP})\\ \\ &=&\vec{OA}+\vec{OB}-2\vec{OP}\\ \\ &=&(0,\ 2)+(-\sqrt{3},\ -1)-2(a,\ b)\\ \\ &=&(-2a-\sqrt{3},\ -2b+1) \end{eqnarray*}
\begin{eqnarray*} \vec{PE} &=&\vec{PO}+\vec{PC}\\ \\ &=&-\vec{OP}+\vec{OC}-\vec{OP}\\ \\ &=&\vec{OC}-2\vec{OP}\\ \\ &=&(\sqrt{3},\ -1)-2(a,\ b)\\ \\ &=&(-2a+\sqrt{3},\ -2b-1) \end{eqnarray*} $よって$
\begin{eqnarray*} \vec{PD}\cdot \vec{PE} \\ &=&(-2a-\sqrt{3},\ -2b+1) \cdot (-2a+\sqrt{3},\ -2b-1)\\ \\ &=&(-2a-\sqrt{3})(-2a+\sqrt{3})+(-2b+1)(-2b-1)\\ \\ &=&4(a^2+b^2)-4\\ \\ &=&0 \end{eqnarray*} $したがって、内積\ \ \vec{PD}\cdot \vec{PE}\ \ は点P\ の位置によらず一定で、その値は \ \ 0$
$なお、このことから \quad \vec{PD} \perp \vec{PE} \quad であることがわかる。$
(2)
$\vec{OD}=\vec{OP}+\vec{PD}=(a,\ b)+(-2a-\sqrt{3},\ -2b+1)=(-a-\sqrt{3},\ -b+1)$
$\vec{OE}=\vec{OP}+\vec{PE}=(a,\ b)+(-2a+\sqrt{3},\ -2b-1)=(-a+\sqrt{3},\ -b-1)$
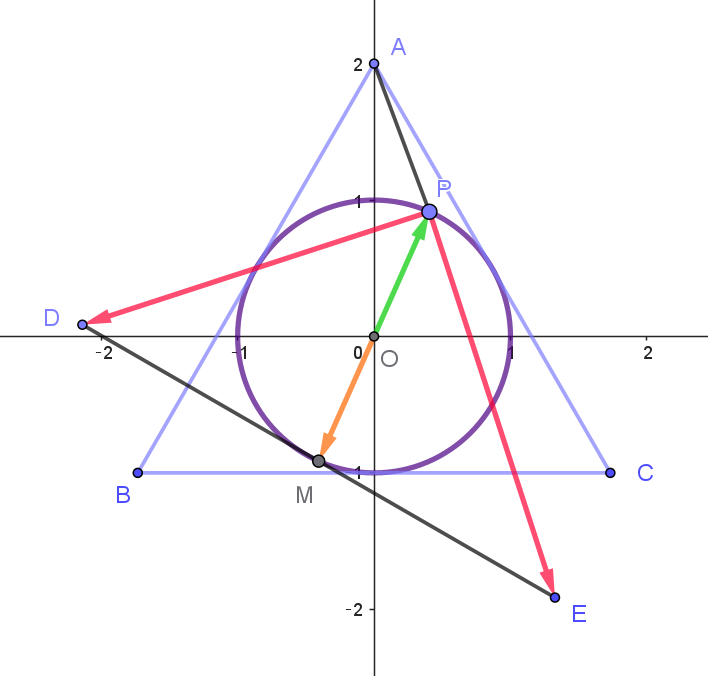
$\vec{OM}=\dfrac{1}{2}(\vec{OD}+\vec{OE})=\dfrac{1}{2}(-2a,\ -2b)=-(a,\ b)=-\vec{OP}$
$点P\ が三角形ABC\ の内接円上を \ 1\ 周すると、点M\ は点P\ と原点に$
$ついて対称な点だから、やはりこの円周上を \ 180°\ ずれて \ 1\ 周する。$
メインメニュー に戻る